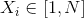Translate quaternion rotation to correct frame

Question

I place an IMU on my wrist and extend my arm as shown in the photo below. I spin in a circle once, while my arm remains in the fixed position. I calculate the euler pitch and quaternion angle. In the photo below, the euler pitch remains approximately constant ( my hand shakes a bit ), while the quaternion angle increases linearly it seems. My data is located here: (sample_data.csv)

Question:

What changes should I make to measure the angle from the quaternion? ( I suspect it is in form of RPR', adjust to world axis, but am unsure what P would be )

Matlab code:

clc;
clear;

table = readtable("sample_data.csv", 'Delimiter', ',');
euler_angles = zeros(length(table.w),1);
quaternion_angles = zeros(length(table.w),1);

for idx = 1:length(table.w)
    w = table.w(idx);
    x = table.x(idx);
    y = table.y(idx);
    z = table.z(idx);
    euler_angles(idx) = getEulerAngle(w,x,y,z);
    quaternion_angles(idx) = getQuaternionAngle(w,x,y,z);
end

figure(1);
clf;
hold on;
plot(euler_angles,'ro');
ylabel("Angle in deg");
xlabel("Sample");
plot(quaternion_angles, 'bo');
hold off;
legend('Euler','Quaternion');

function angle = getQuaternionAngle(w,x,y,z)
    q = quaternion(w,x,y,z);
    angle = acosd(w);
end

function angle = getEulerAngle(w, x, y, z)
    mag = (2*(y * w - z * x));
    angle = rad2deg(asin(mag));
end

Hi, what is an "angle of a quaternion" ?? What does that mean? — Fattie, Jul 06 '22 at 12:18
it is my interpretation of what the authors of the post wrote. the equivalent of yaw for example, is zeroing out two axis and re-normalizing the quaternion to extract the “angle” of rotation. — angryip, Jul 06 '22 at 12:55
the four elements of a quaternion are not axis. (it's very confusing they are usually labelled xyz) — Fattie, Jul 06 '22 at 14:28

BillBokeey · Accepted Answer · 2022-07-06T14:10:56.760

2

Assuming you rotate around an axis [x;y;z] , the post you refer to states that the quaternion associated with the rotation is of the form:

q(1) = cos(r/2);
q(2) = sin(r/2)*x;
q(3) = sin(r/2)*y;
q(4) = sin(r/2)*z;

Where r is the angle in radians and [x;y;z] is the 3d vector representing the axis around which you rotate.

To get the instantaneous rotation r you need to calculate 2*acos(q(1)) for an angle in radians, or 2*acosd(q(1)) for an angle in degrees.

Now plotting the data from your csv file gives the following:

Which is coherent with the assumption that w is the first coordinate of your quaternion, and that you indeed rotate mostly around z.

Euler angles (Or more likely Tait Bryan angles) are a different way to represent a rotation. A rotation is represented by a composition of 3 elemental rotations. These 3 rotations are sometimes called yaw, pitch and roll. If you want to fully represent your rotation, you will have to calculate all of these 3 elemental rotations:

table = readtable("sample_data.csv", 'Delimiter', ',');

w = table.w;
x = table.x;
y = table.y;
z = table.z;

[yaw,pitch,roll] = getAngles(w, x, y, z);

quaternion_angles = getQuaternionAngle(w);

figure; plot([quaternion_angles,yaw,pitch,roll]);

legend({'quat','yaw','pitch','roll'})

function angle = getQuaternionAngle(w)

    angle = 2*acosd(w);
    
end

function [yaw,pitch,roll] = getAngles(w, x, y, z)
    
    yaw = atan2d(2*(y.*z + w.*x), w.*w - x.*x - y.*y + z.*z);
    pitch = asind(-2*(x.*z-w.*y));
    roll = atan2d(2*(x.*y + w.*z), w.*w + x.*x - y.*y - z.*z);

end

See? The angle around Z is represented by the roll (the discontinuity is due to the use of arctan). When you rotate around yourself, the angle increases steadily between 0 and 360º. You can also see that you have a bit of yaw, i.e your IMU is a bit tilted

edited Jul 06 '22 at 14:10

answered Jul 06 '22 at 12:58

BillBokeey

3,168
14
28

your code is the same as mine, no ( except the multiplication by 2 )? 2*acosd(w) gives a linear trend. I was expecting that the angle would be as straight as the euler version. – angryip Jul 06 '22 at 13:31
So you turn around and expect the angle to be constant? – BillBokeey Jul 06 '22 at 13:37
Your code is almost right, you are just misinterpreting it (And confused about what the angles you calculate represent) – BillBokeey Jul 06 '22 at 13:39
hmm yea, i guess i am confused. it jus seems odd to me that if i keep the arm constant, and all i do is spin in a circle, that the angle is not constant. perhaps the better question then is, is this why i would zero out the x and y components, re-normalize, and then calculate the angle of the w component? ( would it be wrong to expect the output to be a straight line then, like the pitch of euler angles? ) – angryip Jul 06 '22 at 13:52
Well when you rotate, the IMU rotates with you doesn't it? Then why do you find odd to see a rotation? – BillBokeey Jul 06 '22 at 14:18
The angle will only be constant in a frame of reference attached to yourself – BillBokeey Jul 06 '22 at 14:19
that's a good point, and a great illustration. thank you for that. in regards to the last comment, are we saying that if i project the quaternion onto the world frame, the equivalent of the "quaternion pitch" should also be constant? – angryip Jul 06 '22 at 14:27
If I read between the lines correctly : Do you actually want the rotations in a frame of reference attached to yourself, with a direction pointing to your arm? – BillBokeey Jul 06 '22 at 14:53
i might be using the wrong terms. here is what i see in my head. your body is in the world frame. the imu is on your hand, it moves with you. the "pitch" in the world doesnt change, your arm stays constant despite you moving in a circle. i really want to reproduce what the euler rotations pitch is giving me, using quaternions. – angryip Jul 06 '22 at 15:04
The Euler rotation pitch is 0, because, in the frame of reference attached to the ground (not to you!), you don't rotate around anything else than the Z axis. If you were to do the exact same thing (Arm straight, IMU in your hand) in a washing machine, you would have pure pitch and it would not be 0. What I suspect you want to do is represent the rotations in a frame of reference attached to your body, with axes pointing to your head and to your hand. For this the only way is to have 2 IMUs. One attached to your body, "hovering" above your arm, and one in your hand. and then do the difference – BillBokeey Jul 06 '22 at 15:10
would we not be able to solve it using a "static" reference, as opposed to an IMU hovering above your arm? – angryip Jul 06 '22 at 15:45
Well, say you rotate around Z, and then you also rotate your hand with respect to your arm around the same axis. How to you know which is which if you have only one stream of data? – BillBokeey Jul 06 '22 at 15:48
Let us [continue this discussion in chat](https://chat.stackoverflow.com/rooms/246203/discussion-between-angryip-and-billbokeey). – angryip Jul 06 '22 at 15:51

Translate quaternion rotation to correct frame

1 Answers1