How to Find the Minimum Taxicab/Manhattan Distance Between Two Parallel Rectangles?

Question

Given the coordinates of the top left corners of both rectangles, and the coordinates of the bottom right corners of both rectangles, and that the rectangles are parallel to each other, as well as the x and y axis, how do you find the minimum taxicab/manhattan distance between the two rectangles?

Answer 1

It all comes down to categorizing the relationship between the two rectangles. I'll assume they don't intersect. In that case only two situations may occur:

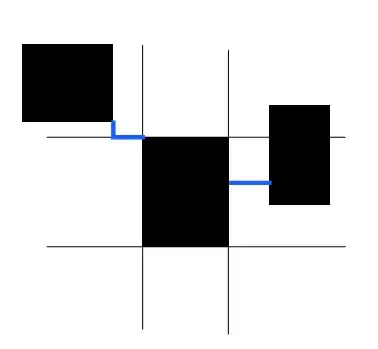
1. The 2nd rectangle is located fully in one of four corner sections of the 1st rectangle
2. All other situations

In the first case you calculate the Manhatten distance between the two opposing corners (TL-BR,TR-BL,BR-TL,BL-TR)

In the second case you take either the difference in x coordinates or the difference in y coordinates of the rectangle sides (B-T,L-R,R-L,T-B) depending on the situation. This is all very easily tested with a few if or case statements.