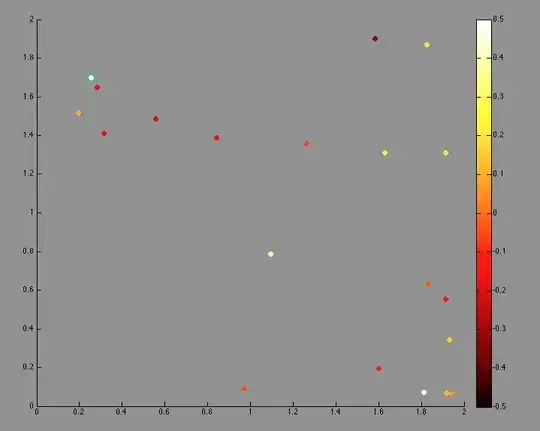
Using Intel MKL's mkl_sparse_d_mv function on our physcs solver to perform a sparse matrix-vector multiplication yields a speedup of between -50% and +25% depending on the sparse matrix used on each case, comparing against the auto-vectorisation case which itself has an inversely correlated performance.
This is not consistent, as it would be desirable to have the same behaviour for (almost) any system configuration and in particular the team expects (sequential) MKL to be overperformant or at least equally performant against auto-vectorisation (using Intel compiler with -O3 on Intel hardware: Xeon Phi's a little bit constrained on memory speed).
Using as a metric the sparsity times the size of the problem shows that the highest mkl_d_sparse_mv performance is for 'the sparsest' system configurations, i.e. mkl performs better when this [*] is relatively small (image attached: ignore the legend, or know that it shows the cubic root of the problem's size).
[*] #rows x (# non-zero-values / # total values)
An example code is below and the question is if the current (i.e. such a variation against O3 auto-vec, or in general a 2x performance variation depending on the sparse matrix's properties: in particular its level of sparsity?) is part of the MKL expected behaviour or is there a not-so-well-known advice that has been missed.
#include <mkl.h>
#include <mkl_spblas.h>
#define ALIGNMENT 64
// An inherited structure in the current SOA-over-AOS paradigm :-/
typedef double TriDouble[3];
// Flag for building sparse matrix only once
static int alreadyBuilt = 0;
// Relevant matrices
static struct matrix_descr descrA;
static MKL_INT EXPECTED_CALLS = (MKL_INT) 5000000;
static sparse_matrix_t csrA1;
static sparse_matrix_t csrA2;
// Sparse matrix sizes
static MKL_INT *m_var;
static MKL_INT *k_var;
static MKL_INT *m2_var;
static MKL_INT *k2_var;
// Data for sparse matrix 1
static double *sparseMatrixElements;
static MKL_INT *sparseMatrixCols;
static MKL_INT *sparseMatrixRowsB;
static MKL_INT *sparseMatrixRowsE;
// Data for sparse matrix 2
static double *sparseMatrixElements2;
static MKL_INT *sparseMatrixCols2;
static MKL_INT * sparseMatrixRowsB2;
static MKL_INT * sparseMatrixRowsE2;
struct problemInformation{
// It's not empty, just too complex for StackOverflow
};
void coreFunction(problemInformation *info)
{
if (alreadyBuilt == 0){
// Allocate memory for columns, values, rows using mkl_malloc
// e.g.
// mkl_malloc()
const int Nrows = 100000;
const int NvalsPerRow = 16;
sparseMatrixElements = (double*) mkl_malloc( sizeof(double) * Nrows * NvalsPerRow, ALIGNMENT);
// Build the matrix using information
int valueN=0;
for (valueN=0; valueN<Nrows*NvalsPerRow; valueN++){
double localVal = 0.0; // Compute it using input information
sparseMatrixElements[valueN] = localVal;
// Etc for rows, columns
}
const int Ncols = 30000; // Compute it using input information
m_var = (MKL_INT*) mkl_malloc(sizeof(MKL_INT), ALIGNMENT);
k_var = (MKL_INT*) mkl_malloc(sizeof(MKL_INT), ALIGNMENT);
m2_var = (MKL_INT*) mkl_malloc(sizeof(MKL_INT), ALIGNMENT);
k2_var = (MKL_INT*) mkl_malloc(sizeof(MKL_INT), ALIGNMENT);
*m_var = (MKL_INT) Nrows;
*k_var = (MKL_INT) Ncols;
*m2_var = (MKL_INT) (Nrows / 3);
*k2_var = (MKL_INT) (Ncols / 3);
descrA.type = SPARSE_MATRIX_TYPE_GENERAL;
// Create matrix 1
sparse_status_t result = mkl_sparse_d_create_csr(&csrA1, SPARSE_INDEX_BASE_ZERO, *m_var, *k_var, sparseMatrixRowsB, sparseMatrixRowsE, sparseMatrixCols, sparseMatrixElements);
if (result != SPARSE_STATUS_SUCCESS) {printf("ERROR IN CREATING MATRIX A1"); fflush(NULL); exit(1);}
// Create matrix 2
result = mkl_sparse_d_create_csr(&csrA2, SPARSE_INDEX_BASE_ZERO, *m2_var, *k2_var, sparseMatrixRowsB2, sparseMatrixRowsE2, sparseMatrixCols2, sparseMatrixElements2);
if (result != SPARSE_STATUS_SUCCESS) {printf("ERROR IN CREATING MATRIX A2"); fflush(NULL); exit(1);}
// Set memory hint: how many times will it be used for matrix-vector multiplication.
result = mkl_sparse_set_symgs_hint(csrA1, SPARSE_OPERATION_NON_TRANSPOSE, descrA, EXPECTED_CALLS);
if (result != SPARSE_STATUS_SUCCESS) {printf("ERROR IN SETTING MEMORY HINT FOR MATRIX A1"); fflush(NULL); exit(1);}
result = mkl_sparse_set_symgs_hint(csrA2, SPARSE_OPERATION_NON_TRANSPOSE, descrA, EXPECTED_CALLS);
if (result != SPARSE_STATUS_SUCCESS) {printf("ERROR IN SETTING MEMORY HINT FOR MATRIX A2"); fflush(NULL); exit(1);}
// Call mkl_sparse_optimize: should we sort CSR column indices or is that included???
result = mkl_sparse_optimize(csrA1);
if (result != SPARSE_STATUS_SUCCESS) {printf("ERROR IN MATRIX A1 OPTIMIZATION"); fflush(NULL); exit(1);}
result = mkl_sparse_optimize(csrA2);
if (result != SPARSE_STATUS_SUCCESS) {printf("ERROR IN MATRIX A2 OPTIMIZATION"); fflush(NULL); exit(1);}
alreadyBuilt = 1;
}
const double alpha=1.0;
const double alpha=0.0;
const int OFFSET1=0; // Computed from input information
const int OFFSET2=0; // Computed from input information
const int OFFSET3=0; // Computed from input information
const int OFFSET4=0; // Computed from input information
// Observation 1: copying the input variables "u", "T", "grad_u", "grad_T" into a mkl_malloc allocated
// chunk of 64-aligned memory decreases performance a little bit
// Clock this
mkl_sparse_d_mv(SPARSE_OPERATION_NON_TRANSPOSE, alpha, csrA1, descrA, &u[OFFSET1][OFFSET2], beta, &grad_u[OFFSET3][0][0]);
mkl_sparse_d_mv(SPARSE_OPERATION_NON_TRANSPOSE, alpha, csrA2, descrA, &T[OFFSET4], beta, &grad_T[OFFSET3][0]);
// Also clock the old version
//
// Old version goes here...
// Print the results of the timer
}
int main (void)
{
TriDouble *rhs;
TriDouble *lhs;
build_rhs(rhs); // Call a C++ function that allocates memory using
// new TriDouble[desired_length]
build_lhs(lhs); // idem
problemInformation info; // Initialize the problem's information parsing the command line arguments etc.
const int EPOCHS = 10000;
int i=0;
for (; i< EPOCHS; i++){
coreFunction(info); // Call the core function 10000 times
}
return 0;
}
The previous code is an excellent minimal example of our current setting, but it does not compile as it lacks several relevant declarations.
A working example using mkl_sparse_d_mv is as follows from the official tutorial, albeit it has not been here tested in performance against automatic vectorisation using the relevant matrices.
/*******************************************************************************
* Copyright 2013-2018 Intel Corporation.
*
* This software and the related documents are Intel copyrighted materials, and
* your use of them is governed by the express license under which they were
* provided to you (License). Unless the License provides otherwise, you may not
* use, modify, copy, publish, distribute, disclose or transmit this software or
* the related documents without Intel's prior written permission.
*
* This software and the related documents are provided as is, with no express
* or implied warranties, other than those that are expressly stated in the
* License.
*******************************************************************************/
/*
* Content : Intel(R) MKL IE Sparse BLAS C example for mkl_sparse_d_mv
*
********************************************************************************
*
* Consider the matrix A (see 'Sparse Storage Formats for Sparse BLAS Level 2
* and Level 3 in the Intel(R) MKL Reference Manual')
*
* | 1 -1 0 -3 0 |
* | -2 5 0 0 0 |
* A = | 0 0 4 6 4 |,
* | -4 0 2 7 0 |
* | 0 8 0 0 -5 |
*
* The matrix A is represented in a zero-based compressed sparse row (CSR) storage
* scheme with three arrays (see 'Sparse Matrix Storage Schemes' in the
* Intel(R) MKL Reference Manual) as follows:
*
* values = ( 1 -1 -3 -2 5 4 6 4 -4 2 7 8 -5 )
* columns = ( 0 1 3 0 1 2 3 4 0 2 3 1 4 )
* rowIndex = ( 0 3 5 8 11 13 )
*
* The test computes the following operations :
*
* A*x = y using mkl_sparse_d_mv
* where A is a general sparse matrix and x and y are vectors
*
********************************************************************************
*/
#include <stdio.h>
#include <assert.h>
#include <math.h>
#include "mkl_spblas.h"
int main() {
//*******************************************************************************
// Declaration and initialization of parameters for sparse representation of
// the matrix A in the compressed sparse row format:
//*******************************************************************************
#define M 5
#define N 5
#define NNZ 13
//*******************************************************************************
// Sparse representation of the matrix A
//*******************************************************************************
double csrVal[NNZ] = { 1.0, -1.0, -3.0,
-2.0, 5.0,
4.0, 6.0, 4.0,
-4.0, 2.0, 7.0,
8.0, -5.0 };
MKL_INT csrColInd[NNZ] = { 0, 1, 3,
0, 1,
2, 3, 4,
0, 2, 3,
1, 4 };
MKL_INT csrRowPtr[M+1] = { 0, 3, 5, 8, 11, 13 };
// Descriptor of main sparse matrix properties
struct matrix_descr descrA;
// // Structure with sparse matrix stored in CSR format
sparse_matrix_t csrA;
//*******************************************************************************
// Declaration of local variables:
//*******************************************************************************
double x[N] = { 1.0, 5.0, 1.0, 4.0, 1.0};
double y[N] = { 0.0, 0.0, 0.0, 0.0, 0.0};
double alpha = 1.0, beta = 0.0;
MKL_INT i;
printf( "\n EXAMPLE PROGRAM FOR mkl_sparse_d_mv \n" );
printf( "---------------------------------------------------\n" );
printf( "\n" );
printf( " INPUT DATA FOR mkl_sparse_d_mv \n" );
printf( " WITH GENERAL SPARSE MATRIX \n" );
printf( " ALPHA = %4.1f BETA = %4.1f \n", alpha, beta );
printf( " SPARSE_OPERATION_NON_TRANSPOSE \n" );
printf( " Input vector \n" );
for ( i = 0; i < N; i++ )
{
printf( "%7.1f\n", x[i] );
};
// Create handle with matrix stored in CSR format
mkl_sparse_d_create_csr ( &csrA, SPARSE_INDEX_BASE_ZERO,
N, // number of rows
M, // number of cols
csrRowPtr,
csrRowPtr+1,
csrColInd,
csrVal );
// Create matrix descriptor
descrA.type = SPARSE_MATRIX_TYPE_GENERAL;
// Analyze sparse matrix; choose proper kernels and workload balancing strategy
mkl_sparse_optimize ( csrA );
// Compute y = alpha * A * x + beta * y
mkl_sparse_d_mv ( SPARSE_OPERATION_NON_TRANSPOSE,
alpha,
csrA,
descrA,
x,
beta,
y );
// Release matrix handle and deallocate matrix
mkl_sparse_destroy ( csrA );
printf( " \n" );
printf( " OUTPUT DATA FOR mkl_sparse_d_mv \n" );
// y should be equal { -16.0, 23.0, 32.0, 26.0, 35.0 }
for ( i = 0; i < N; i++ )
{
printf( "%7.1f\n", y[i] );
};
printf( "---------------------------------------------------\n" );
return 0;
}