-1

I am using XGBoost classifier that classify X-ray images into 3 classes. My problem is that when I calculate these values manually (by hand) using the confusion matrix, it shows me values that are not as they are in the classification report. Even though I used all the equations to calculate those. Please I need a help on how I can make a calculation by hand to find these values (accuracy, precision and recall).

here is the classification report

    precision    recall  f1-score   support

           0     1.0000    0.9052    0.9502       116
           1     0.8267    0.9180    0.8700       317
           2     0.9627    0.9357    0.9490       855

accuracy                             0.9286      1288
macro avg        0.9298    0.9196    0.9231      1288
weighted avg     0.9326    0.9286    0.9297      1288

and this is the confusion matrix

[0.90     0.05     0.04

 0        0.91     0.08

 0        0.06     0.93]
SAT
  • 1
  • 2

1 Answers1

0

enter image description here

Accuracy

How many of the correct predictions are made in total? (Closer to 1)

enter image description here

TP plus TN, divided by the sum of all

Recall

In a sample that is actually positive, the proportion of samples that are determined to be positive

enter image description here

How many of the total things I'm trying to get right? (Closer to 1)

Precision

If it is predicted to be positive, moderate positive. How accurate the positive prediction is

enter image description here

How many correct answers are correct among the questions you solved? (Closer to 1 is better)

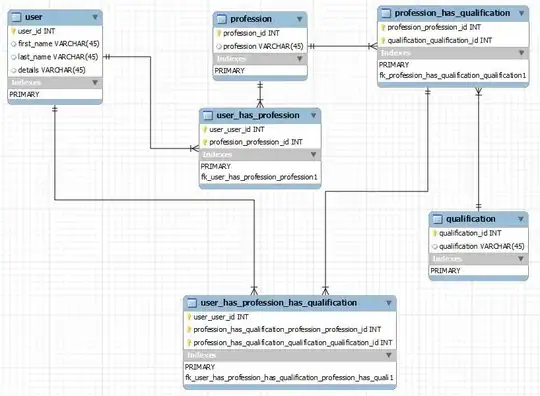
Okay lets do 3 x 3 confusion matrix

enter image description here

class A precision = 15 / 24 = 0.625

class B precision = 15 / 20 = 0.75

class C precision = 45 / 56 = 0.80

class A recall = 15 / 20 = 0.75

class B recall = 15 / 30 = 0.5

class C recall = 45 / 50 = 0.9

Accuracy of classifier = (15 + 15 + 45) / 100 = 0.75

Weighted Average Precision = Actual class A instances * precison of class A + Actual class B instances * precison of class B + Actual class C instances * precison of class C
= 20 / 100 * 0.625 + 30 / 100 * 0.75 + 50 / 100 * 0.8 = 0.75

Weighted Average Recall = Actual class A instances * Recall of class A + Actual class B instances * Recall of class B + Actual class C instances * Recall of class C
= 20 / 100 * 0.75 + 30 / 100 * 0.5 + 50 / 100 * 0.9 = 0.75

In your case

enter image description here

class A precision = 0.9 / 0.9 = 1

class B precision = 0.91 / 1.02 = 0.89

class C precision = 0.93 / 1.05 = 0.89

class A recall = 0.9 / 0.99 = 0.91

class B recall = 0.91 / 0.99 = 0.92

class C recall = 0.93 / 0.99 = 0.94

Accuracy of classifier = (0.9 + 0.91 + 0.93) / 2.97 = 0.92

Weighted Average Precision = Actual class A instances * precison of class A + Actual class B instances * precison of class B + Actual class C instances * precison of class C = 0.99 / 2.97 * 1 + 0.99 / 2.97 * 0.89 + 0.99 / 2.97 * 0.89 = 0.93

Weighted Average Recall = Actual class A instances * Recall of class A + Actual class B instances * Recall of class B + Actual class C instances * Recall of class C = 0.99 / 2.97 * 0.91 + 0.99 / 2.97 * 0.92 + 0.99 / 2.97 * 0.94 = 0.92

Tae In Kim
  • 194
  • 2
  • 13
  • Hi Tae In Kim , Did you apply these formula on the confusion matrix? I don't think so. ..... I had been used these formula many times previously, but I didn't reach to the correct values like in classification report – SAT Jun 16 '22 at 06:05
  • I edited it. Check the 3x3 confusion matrix – Tae In Kim Jun 16 '22 at 08:17
  • I am very grateful for your help in solving this issue... I only have one question . The precision of class A and B is not as shown in the report... How can it be calculated more accurately as found in the classification report report precison of class B = 0.8267 and precision of Class C = 0.9627 thank you. – SAT Jun 16 '22 at 10:05
  • This is the answer to your question. Check your code – Tae In Kim Jun 16 '22 at 14:15