My aim is to use GSL monte carlo integration for an integrand in which an arbitrary multiprecision library (Boost) is used. I decided to use an arbitrary multiprecision library because the integral had difficulties to reach convergence.
This is the actual mathematical formula describing what I am trying to code. My guess is that I do not reach convergence and therefore NaN because 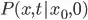 and
and  can get very small values, near zeros.
can get very small values, near zeros.


This is my code:
mp::float128 PDFfunction(double invL, int t, double invtau, double x0, double x, int n_lim) {
const double c = M_PI * (M_PI/4) * ((2 * t) * invtau);
mp::float128 res = 0;
for(int n = 1; n <= n_lim; ++n){
res += exp(-1 * (n * n) * c) * cos((n * M_PI * x) * invL) * cos((n * M_PI * x0) * invL);
}
mp::float128 res_tot = invL + ((2 * invL) * res);
return res_tot;
}
The following lines define the integral that I carry out using GSL:
struct my_f_params {double x0; double xt_pos; double y0; double yt_pos; double invLx; double invLy;
double invtau_x; double invtau_y; int n_lim; double tax_rate;};
double g(double *k, size_t dim, void *p){
struct my_f_params * fp = (struct my_f_params *)p;
mp::float128 temp_pbx = prob1Dbox(fp->invLx, k[0], fp->invtau_x, fp->x0, fp->xt_pos, fp->n_lim);
mp::float128 temp_pby = prob1Dbox(fp->invLy, k[0], fp->invtau_y, fp->y0, fp->yt_pos, fp->n_lim);
mp::float128 AFac = (-2 * k[0] * fp->tax_rate);
mp::float128 res = exp(log(temp_pbx) + log(temp_pby) + AFac);
return res.convert_to<double>();
}
double integrate_integral(const double& x0, const double& xt_pos, const double& y0,
const double& yt_pos, const double& invLx, const double& invLy, const double& invtau_x,
const double& invtau_y, const int& n_lim, const double& tax_rate){
double res, err;
double xl[1] = {0};
double xu[1] = {10000000};
const gsl_rng_type *T;
gsl_rng *r;
gsl_monte_function G;
struct my_f_params params = {x0, xt_pos, y0, yt_pos, invLx, invLy, invtau_x, invtau_y, n_lim, tax_rate};
G.f = &g;
G.dim = 1;
G.params = ¶ms;
size_t calls = 10000;
gsl_rng_env_setup ();
T = gsl_rng_default;
r = gsl_rng_alloc (T);
gsl_monte_vegas_state *s = gsl_monte_vegas_alloc (1);
gsl_monte_vegas_integrate (&G, xl, xu, 1, 10000, r, s,
&res, &err);
do
{
gsl_monte_vegas_integrate (&G, xl, xu, 1, calls/5, r, s,
&res, &err);
}
while (fabs (gsl_monte_vegas_chisq (s) - 1.0) > 0.5);
gsl_monte_vegas_free (s);
gsl_rng_free (r);
return res;
}
When I try to run integral_integrate with x0 = 0; xt_pos = 0; y0 = 0; yt_pos = 10; invLx = invLy = 0.09090909; invtau_x = invtau_y = 0.000661157; n_lim = 1000; tax_rate = 7e-8; I get NaN. Why is this the case? I was not expecting this result since I used Log-Sum-Exp to get rid of possible underflow.