Writing a log-likelihood as a function in R (what is theta?)

Question

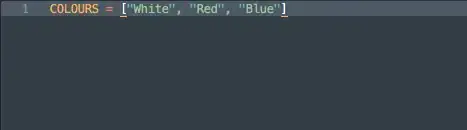
I have the following log-likelihood from my model which i am trying to write as a function in R.

My issue come as i dont know how to write theta in terms of the the function. I have had a couple of attempts at this as shown below, any tips/advice on if these are close to being correct could be appreciated.

function with theta written as theta

#my likelihood function
mylikelihood = function(beta) {

#log-likelihood
result = sum(log(dengue$cases + theta + 1 / dengue$cases)) +
  sum(theta*log(theta / theta + exp(beta[1]+beta[2]*dengue$time))) + 
  sum(theta * log(exp(beta[1]+beta[2]*dengue$time / dengue$cases + exp(beta[1]+beta[2]*dengue$time))))

#return negative log-likelihood
return(-result)
}

my next attempt with thetas replaced with Xi from my dataset, which here is (dengue$time)

#my likelihood function attempt 2
mylikelihood = function(beta) {

#log-likelihood
result = sum((log(dengue$Cases + dengue$Time + 1 / dengue$Cases))) +
sum(dengue$Time*log(dengue$time / dengue$Time + exp(beta[1]+beta[2]*dengue$Time))) + 
sum(dengue$Cases * log(exp(beta[1]+beta[2]*dengue$Time / dengue$Cases + 
exp(beta[1]+beta[2]*dengue$Time))))

 #return negative log-likelihood
 return(-result)
 }

data

   head(dengue)
  Cases Week Time
1   148   36    1
2   275   37    2
3   205   38    3
4   133   39    4
5   123   40    5
6   138   41    6

Are either of these close to being correct, and if not where am I going wrong?

Updated into about where the log-likelihood comes from;

The model;

Negative Binomial distribution with mean µ and dispersion parameter θ has pmf;

Answer 1

The fundamental problem is that you have to pass both beta (intercept and slope of one component of the problem) and theta as part of a single parameter vector. You had other problems with parenthesis placement that I fixed, and I reorganized the expressions a little bit.

There are several more important mistakes in your code.

• The first term is not a fraction; it is a binomial coefficient. (i.e., you should use lchoose(), as shown below)
• You changed a +1 to a -1 in the first term.

nll <- function(pars) {                                                                                      
    beta <- pars[1:2]                                                                                        
    theta <- pars[3]                                                                                         
                                                                                                             
    ##log-likelihood                                                                                         
    yi <- dengue$Cases                                                                                       
    xi <- dengue$Time                                                                                        
    ri <- exp(beta[1]+beta[2]*xi)                                                                            
    result <- sum(lchoose(yi + theta - 1,yi)) +                                                              
        sum(theta*log(theta / (theta + ri))) +                                                               
        sum(yi * log(ri/(theta+ri)))                                                                         
    ##return negative log-likelihood                                                                         
    return(-result)                                                                                          
}                                                                                                            

read data

dengue <- read.table(row.names = 1, header = TRUE, text = "                                                  
 Cases Week Time                                                                                             
1   148   36    1                                                                                            
2   275   37    2                                                                                            
3   205   38    3                                                                                            
4   133   39    4                                                                                            
5   123   40    5                                                                                            
6   138   41    6                                                                                            
")         

fitting

Guessing starting parameters of (1,1,1) is a bit dangerous - it would make more sense to know something about the meaning of the parameters and guess biologically plausible values - but it seems to be OK.

nll(c(1,1,1))                                                                                                
optim(par = c(1,1,1), nll)                                                                                   

Since we didn't constrain theta to be positive we get some warnings about taking the log of a negative number, but these are probably harmless (e.g. see here)

---

alternatives

R has a lot of built-in machinery for fitting negative binomial models (I should have recognized what you were doing!)

MASS::glm.nb sets everything up for you automatically, you just have to specify the predictor variables (it uses a logarithmic link and adds an intercept, so specifying ~Time will make the mean equal to exp(beta0 + beta1*Time)).

library(MASS)
glm.nb(Cases ~ Time, data = dengue)

bbmle is a little bit less automated, but more flexible (here I am fitting theta on the log scale to avoid trying any negative values)

library(bbmle)
mle2(Cases ~ dnbinom(mu = exp(logmu), size = exp(logtheta)),
                     parameters = list(logmu ~ Time),
                     data = dengue,
                     start = list(logmu = 0, logtheta = 0))

All three of these approaches (corrected negative log-likelihood function + optim, MASS::glm.nb, bbmle::mle2) give the same results.