Have I applied the Fourier Transformation correctly to this Dataframe? [EXAFS X-Ray Absorption Dataframe]

Question

I have a dataset with a signal and a 1/distance (Angstrom^-1) column.

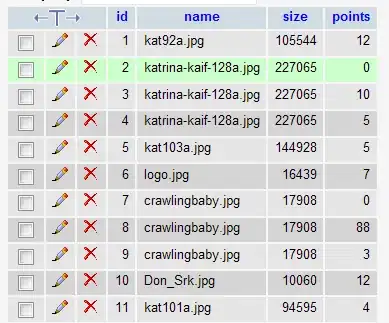
This is the dataset (fourier.csv): https://pastebin.com/ucFekzc6

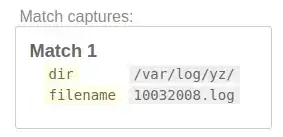
After applying these steps:

import pandas as pd
import numpy as np

from numpy.fft import fft

df = pd.read_csv (r'fourier.csv')

df.plot(x ='1/distance', y ='signal', kind = 'line')

I generated this plot:

To generate the Fast Fourier Transformation data, I used the numpy library for its fft function and I applied it like this:

df['signal_fft'] = fft(df['signal'])

df.plot(x ='1/distance', y ='signal_fft', kind = 'line')

Now the plot looks like this, with the FFT data plotted instead of the initial "signal" data:

What I hoped to generate is something like this (This signal is extremely similar to mine, yet yields a vastly different FFT picture):

Theory Signal before windowing:

Theory FFT:

As you can see, my initial plot looks somewhat similar to graphic (a), but my FFT plot doesn't look anywhere near as clear as graphic (b). I'm still using the 1/distance data for both horizontal axes, but I don't see anything wrong with it, only that it should be interpreted as distance (Angstrom) instead of 1/distance (1/Angstrom) in the FFT plot.

How should I apply FFT in order to get a result that resembles the theoretical FFT curve?

Here's another slide that shows a similar initial signal to mine and a yet again vastly different FFT:

Addendum: I have been asked to provide some additional information on this problem, so I hope this helps.

The origin of the dataset that I have linked is an XAS (X-Ray Absorption Spectroscopy) spectrum of iron oxide. Such an experimentally obtained spectrum looks similar to the one shown in the "Schematic of XAFS data processing" on the top left, i.e. absorbance [a.u.] plotted against the photon energy [eV]. Firstly I processed the spectrum (pre-edge baseline correction + post-edge normalization). Then I converted the data on the x-axis from energy E to wavenumber k (thus dimension 1/Angstrom) and cut off the signal at the L-edge jump, leaving only the signal in the post-edge EXAFS region, referred to as fine structure function χ(k). The mentioned dataset includes k^2 weighted χ(k) (to emphasize oscillations at large k). All of this is not entirely relevant as the only thing I want to do now is a Fourier transformation on this signal ( k^2 χ(k) vs. k). In theory, as we are dealing with photoelectrons and (back)scattering phenomena, the EXAFS region of the XAS spectrum can be approximated using a superposition of many sinusoidal waves such as described in this equation with f(k) being the amplitude and δ(k) the phase shift of the scattered wave.

The aim is to gain an understanding of the chemical environment and the coordination spheres around the absorbing atom. The goal of the Fourier transform is to obtain some sort of signal in dependence of the "radius" R [Angstrom], which could later on be correlated to e.g. an oxygen being in ~2 Angstrom distance to the Mn atom (see "Schematic of XAFS data processing" on the right).

I only want to be able to reproduce the theoretically expected output after the FFT. My main concern is to get rid of the weird output signal and produce something that in some way resembles a curve with somewhat distinct local maxima (as shown in the 4th picture).

Answer 1

I don't have a 100% solution for you, but here's part of the problem.

The fft function you're using assumes that your X values are equally spaced. I checked this assumption by taking the difference between each 1/distance value, and graphing it:

df['1/distance'].diff().plot()

(Y is the difference, X is the index in the dataframe.)

This is supposed to be a constant line.

In order to fix this, one solution is to resample the signal through linear interpolation so that the timestep is constant.

from scipy import interpolate

rs_df = df.drop_duplicates().copy()  # Needed because 0 is present twice in dataset
x = rs_df['1/distance']
y = rs_df['signal']
flinear = interpolate.interp1d(x, y, kind='linear')
xnew = np.linspace(np.min(x), np.max(x), rs_df.index.size)
ylinear = flinear(xnew)

rs_df['signal'] = ylinear
rs_df['1/distance'] = xnew
df.plot(x ='1/distance', y ='signal', kind = 'line')
rs_df.plot(x ='1/distance', y ='signal', kind = 'line')

The new line looks visually identical, but has a constant timestep.

I still don't get your intended result from the FFT, so this is only a partial solution.

Answer 2

MCVE

We import required dependencies:

import numpy as np
import pandas as pd
from scipy import signal
import matplotlib.pyplot as plt

And we load your dataset:

raw = pd.read_csv("https://pastebin.com/raw/ucFekzc6", sep="\t",
                  names=["k", "wchi"], header=0)

We clean the dataset a bit as it contains duplicates and a problematic point with null wave number (or infinite distance) and ensure a zero mean signal:

raw = raw.drop_duplicates()
raw = raw.iloc[1:, :]
raw["wchi"] = raw["wchi"] - raw["wchi"].mean()

The signal is about:

As noticed by @NickODell, signal is not equally sampled which is a problem if you aim to perform FFT signal processing.

We can resample your signal to have equally spaced sampling:

N = 65536
k = np.linspace(raw["k"].min(), raw["k"].max(), N)
interpolant = interpolate.interp1d(raw["k"], raw["wchi"], kind="linear")
g = interpolant(k)

Notice for performance concerns FFT does split the signal with the null frequency component at the borders (that's why your FFT signal does not look as it is usually presented in books). This indeed can be corrected by using classic fftshift method or performing ad hoc indexing.

R = 2*np.pi*fft.fftfreq(N, np.diff(k)[0])[:N//2]
G = (1/N)*fft.fft(g)[0:N//2]

Mind the 2π factor which is involved in the units scaling of your transformation.

You also have mentioned a windowing (at least in a picture) that is not referenced anywhere. This kind of filtering may help a lot when performing signal processing as it filter out artifacts and unwanted noise. I leave it up to you.

Least Square Spectral Analysis

An alternative to process your signal is available since the advent of modern Linear Algebra. There is a way to estimate the periodogram of an irregular sampled signal by a method called Least Square Spectral Analysis.

You are looking for the square root of the periodogram of your signal and scipy does implement an easy way to compute it by the Lomb-Scargle method.

To do so, we simply create a frequency vector (in this case they are desired output distances) and perform the regression for each of those distances w.r.t. your signal:

Rhat = np.linspace(raw["R"].min(), raw["R"].max()*2, 5000)
Ghat = signal.lombscargle(raw["k"], raw["wchi"], freqs=Rhat, normalize=True)

Graphically it leads to:

Comparison

If we compare both methodology we can confirm that the major peaks definitely match.

LSSA gives a smoother curve but do not assume it to be more accurate as this is statistical smooth of an interpolated curve. Anyway it fit the bill for your requirement:

I only want to be able to reproduce the theoretically expected output after the FFT. My main concern is to get rid of the weird output signal and produce something that in some way resembles a curve with somewhat distinct local maxima (as shown in the 4th picture).

Conclusions

I think you have enough information to process your signal either by resampling and using FFT or by using LSSA. Both method has advantages and drawbacks.

Of course this needs to be validated with well know cases. Why not to reproduce with the data of the experience of the paper you are working on to check out you can reconstruct figures you posted.

You also need to dig in the signal conditioning before performing post processing (resampling, windowing, filtering).