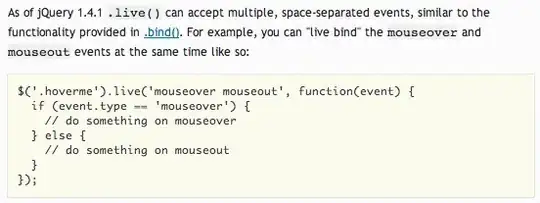
I want to get a 95% confidence interval for the following question.

I have written function f_n in my R code. I first randomly sample 100 with Normal and then I define function h for lambda. Then I can get f_n. My question is that how to define a function of f_n-chi-square and use uniroot` to find Confidence interval.
# I first get 100 samples
set.seed(201111)
x=rlnorm(100,0,2)
Based on the answer by @RuiBarradas, I try the following code.
set.seed(2011111)
# I define function h, and use uniroot function to find lambda
h <- function(lam, n)
{
sum((x - theta)/(1 + lam*(x - theta)))
}
# sample size
n <- 100
# the parameter of interest must be a value in [1, 12],
#true_theta<-1
#true_sd<- exp(2)
#x <- rnorm(n, mean = true_theta, sd = true_sd)
x=rlnorm(100,0,2)
xmax <- max(x)
xmin <- min(x)
theta_seq = seq(from = 1, to = 12, by = 0.01)
f_n <- rep(NA, length(theta_seq))
for (i in seq_along(theta_seq))
{
theta <- theta_seq[i]
lambdamin <- (1/n-1)/(xmax - theta)
lambdamax <- (1/n-1)/(xmin - theta)
lambda = uniroot(h, interval = c(lambdamin, lambdamax), n = n)$root
f_n[i] = -sum(log(1 + lambda*(x - theta)))
}
j <- which.max(f_n)
max_fn <- f_n[j]
mle_theta <- theta_seq[j]
plot(theta_seq, f_n, type = "l",
main = expression(Estimated ~ theta),
xlab = expression(Theta),
ylab = expression(f[n]))
points(mle_theta, f_n[j], pch = 19, col = "red")
segments(
x0 = c(mle_theta, xmin),
y0 = c(min(f_n)*2, max_fn),
x1 = c(mle_theta, mle_theta),
y1 = c(max_fn, max_fn),
col = "red",
lty = "dashed"
)
I got the following plot of f_n.
For 95% CI, I try
LR <- function(theta, lambda)
{
2*sum(log(1 + lambda*(x - theta))) - qchisq(0.95, df = 1)
}
lambdamin <- (1/n-1)/(xmax - mle_theta)
lambdamax <- (1/n-1)/(xmin - mle_theta)
lambda <- uniroot(h, interval = c(lambdamin, lambdamax), n = n)$root
uniroot(LR, c(xmin, mle_theta), lambda = lambda)$root
The result is 0.07198144. Then the logarithm is log(0.07198144)=-2.631347.
But there is NA in the following code.
uniroot(LR, c(mle_theta, xmax), lambda = lambda)$root
So the 95% CI is theta >= -2.631347.
But the question is that the 95% CI should be a closed interval...