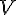How can I construct the new triangles that exist when adding a point to an existing triangle?
Basically if starting with the red triangle, adding the green point, creates 3 triangles. This part I think is pretty straight forward: I would determine what triangle the point falls inside and then create 3 triangles out of the given 4 points.
But what about the purple point? This falls on an edge and creates 4 new triangles.
Is there a way to cover all cases for adding a point and creating new triangles?
And how do I make sure the purple point is on the edge and not slightly away from it?
You can provide an answer in any language, but Lua would be preferred.