How to project a chessboard in camera coordinates to real-world coordinates in OpenCV using rvecs and tvecs outputs of cv.calibrateCamera?

Question

Situation

Following the Camera Calibration tutorial in OpenCV I managed to get an undistorted image of a checkboard using cv.calibrateCamera:

Original image: (named image.tif in my computer)

Code:

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt

# termination criteria
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((12*13,3), np.float32)
objp[:,:2] = np.mgrid[0:12,0:13].T.reshape(-1,2)
# Arrays to store object points and image points from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.

img = cv.imread('image.tif')
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
# Find the chess board corners
ret, corners = cv.findChessboardCorners(gray, (12,13), None)
# If found, add object points, image points (after refining them)

if ret == True:
    objpoints.append(objp)
    corners2 = cv.cornerSubPix(gray,corners, (11,11), (-1,-1), criteria)
    imgpoints.append(corners)
    # Draw and display the corners
    cv.drawChessboardCorners(img, (12,13), corners2, ret)
    cv.imshow('img', img)
    cv.waitKey(2000)

cv.destroyAllWindows()

ret, mtx, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

#Plot undistorted 
h,  w = img.shape[:2]
newcameramtx, roi = cv.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h))

dst = cv.undistort(img, mtx, dist, None, newcameramtx)
# crop the image
x, y, w, h = roi
dst = dst[y:y+h, x:x+w]
plt.figure()
plt.imshow(dst)
plt.savefig("undistorted.png", dpi = 300)
plt.close()

Undistorted image:

The undistorted image indeed has straight lines. However, in order to test the calibration procedure I would like to further transform the image into real-world coordinates using the rvecs and tvecs outputs of cv.calibrateCamera. From the documentation:

• rvecs: Output vector of rotation vectors (Rodrigues ) estimated for each pattern view (e.g. std::vector<cv::Mat>>). That is, each i-th rotation vector together with the corresponding i-th translation vector (see the next output parameter description) brings the calibration pattern from the object coordinate space (in which object points are specified) to the camera coordinate space. In more technical terms, the tuple of the i-th rotation and translation vector performs a change of basis from object coordinate space to camera coordinate space. Due to its duality, this tuple is equivalent to the position of the calibration pattern with respect to the camera coordinate space.

• tvecs: Output vector of translation vectors estimated for each pattern view, see parameter describtion above.

Question: How can I manage this? It would be great if the answers include a working code that outputs the transformed image.

---

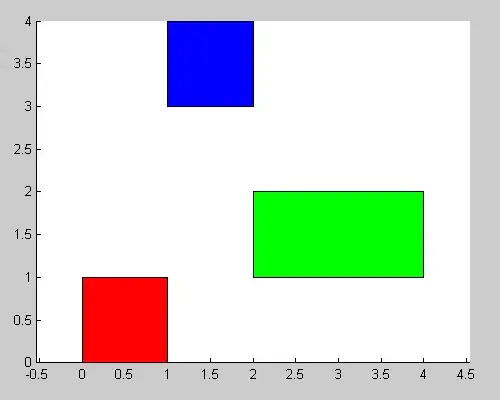
Expected output

The image I expect should look something like this, where the red coordinates correspond to the real-world coordinates of the checkboard (notice the checkboard is a rectangle in this projection):

---

What I have tried

Following the comment of @Christoph Rackwitz, I found this post, where they explain the homography matrix H that relates the 3D real world coordinates (of the chessboard) to the 2D image coordinates is given by:

H = K [R1 R2 t]

where K is the camera calibration matrix, R1 and R2 are the first two columns of the rotational matrix and t is the translation vector.

I tried to calculate this from:

• K we already have it as the mtx from cv.calibrateCamera.
• R1 and R2 from rvecs after converting it to a rotational matrix (because it is given in Rodrigues decomposition): cv.Rodrigues(rvecs[0])[0].
• t should be tvecs.

In order to calculate the homography from the image coordinates to the 3D real world coordinates then I use the inverse of H.

Finally I use cv.warpPerspective to display the projected image.

Code:

R = cv.Rodrigues(rvecs[0])[0]
tvec = tvecs[0].squeeze()
H = np.dot(mtx, np.concatenate((R[:,:2], tvec[:,None]), axis = 1) )/tvec[-1] 
plt.imshow(cv.warpPerspective(dst, np.linalg.inv(H), (dst.shape[1], dst.shape[0])))

But this does not work, I find the following picture:

Any ideas where the problem is?

---

Related questions:

• How do I obtain the camera world position from calibrateCamera results?
• Homography from 3D plane to plane parallel to image plane
• OpenCV Camera Calibration mathematical background
• Coordinate transformation in OpenCV
• transform 3d camera coordinates to 3d real world coordinates with opencv

Answer 1

Every camera has its own Intrinsic parameters connecting 2D image coordinates with 3D real-world. You should solve a branch of linear equations to find them out. Or look at cameras specification parameters, provided by manufacturers.
Furthermore, if you want to warp your surface to be parallel to the image border use homography transformations. You need the projective one. scikit-image has prepaired tools for parameter estimation.

Answer 2

The Concept

Detect the corners of the chessboard using the cv2.findChessboardCorners() method. Then, define an array for the destination point for each corner point in the image. Use the triangle warping technique to warp the image from the chessboard corner points to the points in the array defined for the destination locations.

The Code

import cv2
import numpy as np

def triangles(points):
    points = np.where(points, points, 1)
    subdiv = cv2.Subdiv2D((*points.min(0), *points.max(0)))
    for pt in points:
        subdiv.insert(tuple(map(int, pt)))
    for pts in subdiv.getTriangleList().reshape(-1, 3, 2):
        yield [np.where(np.all(points == pt, 1))[0][0] for pt in pts]

def crop(img, pts):
    x, y, w, h = cv2.boundingRect(pts)
    img_cropped = img[y: y + h, x: x + w]
    pts[:, 0] -= x
    pts[:, 1] -= y
    return img_cropped, pts

def warp(img1, img2, pts1, pts2):
    img2 = img2.copy()
    for indices in triangles(pts1):
        img1_cropped, triangle1 = crop(img1, pts1[indices])
        img2_cropped, triangle2 = crop(img2, pts2[indices])
        transform = cv2.getAffineTransform(np.float32(triangle1), np.float32(triangle2))
        img2_warped = cv2.warpAffine(img1_cropped, transform, img2_cropped.shape[:2][::-1], None, cv2.INTER_LINEAR, cv2.BORDER_REFLECT_101)
        mask = np.zeros_like(img2_cropped)
        cv2.fillConvexPoly(mask, np.int32(triangle2), (1, 1, 1), 16, 0)
        img2_cropped *= 1 - mask
        img2_cropped += img2_warped * mask
    return img2

img = cv2.imread("image.png")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
ret, corners = cv2.findChessboardCorners(gray, (12 ,13), None)
corners2 = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)

x, y, w, h, r, c = 15, 40, 38, 38, 12, 13
pts1 = np.int32(corners2.squeeze())
arr2 = np.tile(np.arange(c), r).reshape((r, c))
arr1 = np.tile(np.arange(r), c).reshape((c, r))
arr = np.dstack((arr1[:, ::-1] * h + y, arr2.T * w + x))
pts2 = arr.reshape((r * c, 2))

cv2.imshow("result", warp(img, np.zeros_like(img), pts1, pts2))
cv2.waitKey(0)

The Output

Here is the output image:

For the input image of:

The Explanation

1. Import the necessary libraries:

import cv2
import numpy as np

2. Define a function, triangles, that will take in an array of coordinates, points, and yield lists of 3 indices of the array for triangles that will cover the area of the original array of coordinates:

def triangles(points):
    points = np.where(points, points, 1)
    subdiv = cv2.Subdiv2D((*points.min(0), *points.max(0)))
    for pt in points:
        subdiv.insert(tuple(map(int, pt)))
    for pts in subdiv.getTriangleList().reshape(-1, 3, 2):
        yield [np.where(np.all(points == pt, 1))[0][0] for pt in pts]

3. Define a function, crop, that will take in an image array, img, and an array of three coordinates, pts. It will return a rectangular segment of the image just large enough to fit the triangle formed by the three point, and return the array of three coordinates transferred to the top-left corner of image:

def crop(img, pts):
    x, y, w, h = cv2.boundingRect(pts)
    img_cropped = img[y: y + h, x: x + w]
    pts[:, 0] -= x
    pts[:, 1] -= y
    return img_cropped, pts

4. Define a function, warp, that will take in 2 image arrays, img1 and img2, and 2 arrays of coordinates, pts1 and pts2. It will utilize the triangles function defined before iterate through the triangles from the first array of coordinates, the crop function defined before to crop both images at coordinates corresponding to the triangle indices and use the cv2.warpAffine() method to warp the image at the current triangle of the iterations:

def warp(img1, img2, pts1, pts2):
    img2 = img2.copy()
    for indices in triangles(pts1):
        img1_cropped, triangle1 = crop(img1, pts1[indices])
        img2_cropped, triangle2 = crop(img2, pts2[indices])
        transform = cv2.getAffineTransform(np.float32(triangle1), np.float32(triangle2))
        img2_warped = cv2.warpAffine(img1_cropped, transform, img2_cropped.shape[:2][::-1], None, cv2.INTER_LINEAR, cv2.BORDER_REFLECT_101)
        mask = np.zeros_like(img2_cropped)
        cv2.fillConvexPoly(mask, np.int32(triangle2), (1, 1, 1), 16, 0)
        img2_cropped *= 1 - mask
        img2_cropped += img2_warped * mask
    return img2

5. Read in the image of the distorted chessboard, convert it to grayscale and detect the corners of the chessboard:

img = cv2.imread("image.png")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
ret, corners = cv2.findChessboardCorners(gray, (12 ,13), None)
corners2 = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)

6. Define an array of the destination points for each corner detected. If you plot each corner along with their corresponding index in the array, you will see that they are in this order:

So our destination array must be in that order, or we will end up with unreadable results. The x, y, w, h, r, c below will be the destination array of coordinates' top-left x, y position, each square's width & height, and the number of rows & columns of points in the board:

x, y, w, h, r, c = 15, 40, 38, 38, 12, 13
pts1 = np.int32(corners2.squeeze())
arr2 = np.tile(np.arange(c), r).reshape((r, c))
arr1 = np.tile(np.arange(r), c).reshape((c, r))
arr = np.dstack((arr1[:, ::-1] * h + y, arr2.T * w + x))
pts2 = arr.reshape((r * c, 2))

6. Finally, show the warped part of the image on a blank image:

cv2.imshow("result", warp(img, np.zeros_like(img), pts1, pts2))
cv2.waitKey(0)

Answer 3

At the end, I did not manage to achieve it with the outputs of cv.calibrateCamera but instead I did something simple inspired by @Ann Zen answer. In case it may help someone I will just post it here.

I transform both the image and some data points in the image to the new coordinates given by the chessboard reference frame using only the four corner points.

Input:

undistorted.png

Code:

import numpy as np
import cv2 as cv

image = cv.imread('undistorted.png')

#Paint some points in blue
points = np.array([[200, 300], [400, 300], [500, 200]])
for i in range(len(points)):
    cv.circle(image, tuple(points[i].astype('int64')), radius=0, color=(255, 0, 0), thickness=10)
cv.imwrite('undistorted_withPoints.png', image)

#Put pixels of the chess corners: top left, top right, bottom right, bottom left.
cornerPoints = np.array([[127, 58], [587, 155], [464, 437], [144,344]], dtype='float32')

#Find base of the rectangle given by the chess corners
base = np.linalg.norm(cornerPoints[1] - cornerPoints[0] )

#Height has 11 squares while base has 12 squares.
height = base/12*11

#Define new corner points from base and height of the rectangle
new_cornerPoints = np.array([[0, 0], [int(base), 0], [int(base), int(height)], [0, int(height)]], dtype='float32')

#Calculate matrix to transform the perspective of the image
M = cv.getPerspectiveTransform(cornerPoints, new_cornerPoints)

new_image = cv.warpPerspective(image, M, (int(base), int(height)))

#Function to get data points in the new perspective from points in the image
def calculate_newPoints(points, M):
    new_points = np.einsum('kl, ...l->...k', M,  np.concatenate([points, np.broadcast_to(1, (*points.shape[:-1], 1)) ], axis = -1) )
    return new_points[...,:2] / new_points[...,2][...,None]

new_points = calculate_newPoints(points, M)

#Paint new data points in red
for i in range(len(new_points)):
    cv.circle(new_image, tuple(new_points[i].astype('int64')), radius=0, color=(0, 0, 255), thickness=5)

cv.imwrite('new_undistorted.png', new_image)

Outputs:

undistorted_withPoints.png

new_undistorted.png

Explanation:

• I paint some data points in the original picture that I also want to transform.

• With another program I look for the pixels of the corners of the chess (I skip the outer rows and columns).

• I calculate the height and base in pixels of the rectangle defined by the corners.

• I define from the rectangle the new corners in the chessboard coordinates.

• I calculate the matrix M to do the perspective transformation.

• I do the transformation for the image and for the data points following the documentation of cv.warpPerspective:

• I paint the transformed data points in red.