Plot a 3D figure in a 2D frame

Question

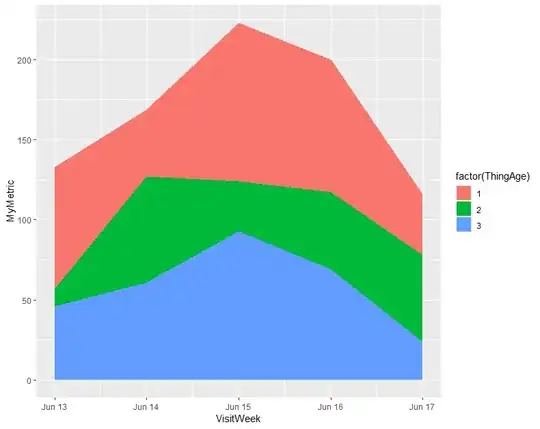
In my current project, I want to plot a 3D shape with pyplot. This is relatively straightforward:

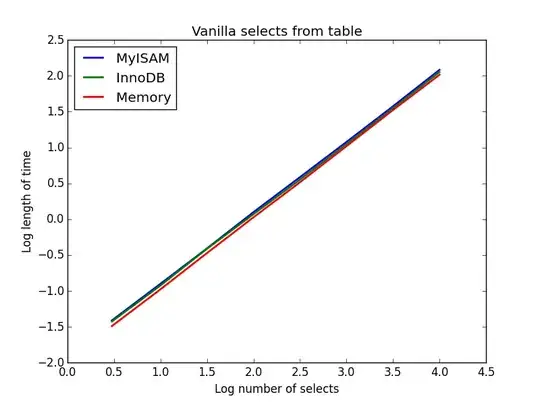
The complication comes from the fact that I would like the figure to display in a straight 2D figure similar to this example:

That is to say, remove the 3D axes and ticks, the gridlines, and wrap everything in a flat 2D border. Is it possible to do this with Pyplot? You can find my code to generate the two figures below:

import matplotlib.pyplot as plt
import numpy as np

plt.figure()

x   = np.asarray([0,1,1.5,0.5,0])
y   = np.asarray([0,0,0.5,0.5,0])

# Plot 2D projection of cube
plt.plot(x,y,color='k')
plt.plot(x,y+1,color='k')
plt.plot([0,0],[0,1],color='k')
plt.plot([1,1],[0,1],color='k')
plt.plot([1.5,1.5],[0.5,1.5],color='k')
plt.plot([0.5,0.5],[0.5,1.5],color='k')

plt.title("2D projection of cube")
plt.axis('equal')
plt.tick_params(left=False,
                bottom=False,
                labelleft=False,
                labelbottom=False)

# Now try the same thing in 3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

x   = np.asarray([0,1,1,0,0])
y   = np.asarray([0,0,1,1,0])

# Plot 2D projection of cube
ax.plot3D(x,y,np.zeros(5),color='k')
ax.plot3D(x,y,np.ones(5),color='k')
ax.plot3D([0,0],[0,0],[0,1],color='k')
ax.plot3D([0,0],[1,1],[0,1],color='k')
ax.plot3D([1,1],[0,0],[0,1],color='k')
ax.plot3D([1,1],[1,1],[0,1],color='k')

plt.title("3D projection of cube")

Ah, yes it is. Both answers were helpful, but neither solved quite what I wanted, so I chose a compromise solution: I used the axis removal of eshirvana's answer, then drew the border artificially with annotation lines. JohanC's answer provided a very useful code which would have been closer to what I had in mind, but unfortunately it was important that the subplot remains 3D. — J.Galt, Mar 12 '22 at 01:55

score 1 · Accepted Answer · answered Mar 08 '22 at 22:34

add these lines :

color_tuple = (1, 1, 1, 0)

# make the panes transparent
ax.xaxis.set_pane_color(color_tuple)
ax.yaxis.set_pane_color(color_tuple)
ax.zaxis.set_pane_color(color_tuple)

# make the axis lines transparent
ax.w_xaxis.line.set_color(color_tuple)
ax.w_yaxis.line.set_color(color_tuple)
ax.w_zaxis.line.set_color(color_tuple)

# make the grid lines transparent
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])

output:

score 1 · Answer 2 · answered Mar 08 '22 at 22:53

The following approach:

describes a cube by 8 vertices and 12 edges
the vertices start in an axis-aligned position
the vertices are rotated around some arbitrary axis; using code from Rotating around a 3D vector
the x and y positions of the rotated vertices are used to draw the cube (so, parallel projection of the rotated cube onto the xy plane)

import matplotlib.pyplot as plt
import numpy as np
import math

def rotation_matrix(axis, theta):
    """
    Return the rotation matrix associated with counterclockwise rotation about
    the given axis by theta radians.
    """
    axis = np.asarray(axis)
    axis = axis / math.sqrt(np.dot(axis, axis))
    a = math.cos(theta / 2.0)
    b, c, d = -axis * math.sin(theta / 2.0)
    aa, bb, cc, dd = a * a, b * b, c * c, d * d
    bc, ad, ac, ab, bd, cd = b * c, a * d, a * c, a * b, b * d, c * d
    return np.array([[aa + bb - cc - dd, 2 * (bc + ad), 2 * (bd - ac)],
                     [2 * (bc - ad), aa + cc - bb - dd, 2 * (cd + ab)],
                     [2 * (bd + ac), 2 * (cd - ab), aa + dd - bb - cc]])

x = np.array([0, 1, 1, 0, 0, 1, 1, 0])
y = np.array([0, 0, 1, 1, 0, 0, 1, 1])
z = np.array([0, 0, 0, 0, 1, 1, 1, 1])
# the 8 vertices of the cube
vertices = np.vstack([x, y, z])
# the 12 edges, each connecting two of the vertices
edges = [[0, 1], [1, 2], [2, 3], [3, 0], [4, 5], [5, 6], [6, 7], [7, 4], [0, 4], [1, 5], [2, 6], [3, 7]]

axis = [4, 3, 0]
theta = 20
rot_vertices = np.dot(rotation_matrix(axis, math.radians(theta)), vertices)
for v0, v1 in edges:
    plt.plot(rot_vertices[0, [v0, v1]], rot_vertices[1, [v0, v1]], color='black')

plt.title("2D projection of cube")
plt.axis('equal')
plt.xticks([])
plt.yticks([])
plt.show()

Plot a 3D figure in a 2D frame

2 Answers2