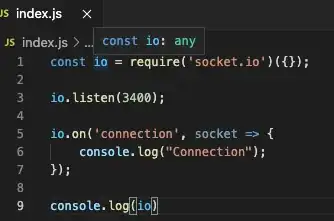
I am working with the R programming language.
In a previous question that I asked (Understanding 3D traces in Plotly and R: Evaluating and Plotting Functions Over a Grid), I learned how to plot mathematical functions by first evaluating the mathematical function at different points, then by plotting these points on a 3D grid, and finally "interpolating" a 3D surface over these points:
# set seed for reproducibility
#load libraries
set.seed(123)
library(dplyr)
library(plotly)
#create more data
n <- 50
my_grid <- expand.grid(i1 = 1:n, i2 = 1:n)
my_grid$final_value = with(my_grid, sin(i1) + cos(i2) )
#make plot
plot_ly(data = my_grid, x=~i1, y=~i2, z=~final_value, type='mesh3d', intensity = ~final_value, colors = colorRamp(c("blue", "grey", "red")))
I am trying to use this same approach to plot the following function (https://en.wikipedia.org/w/index.php?title=Test_functions_for_optimization&oldid=1030693803, https://en.wikipedia.org/w/index.php?title=Test_functions_for_optimization&oldid=1030693803#/media/File:ConstrTestFunc03.png) :
I first defined the function:
my_function <- function(x,y) {
final_value = (1 - x)^2 + 100*((y - x^2)^2)
}
Then, I defined the "grid":
input_1 <- seq(-1.5, 1.5,0.1)
input_2 <- seq(-1.5, 1.5,0.1)
my_grid <- data.frame(input_1, input_2)
my_grid$final_value = (1 - input_1)^2 + 100*((input_2 - input_1^2)^2)
Then, I tried to plot this function:
x <- my_grid$input_1
y <- my_grid$input_2
z <- matrix(my_grid$final_value, nrow = length(x), ncol = length(y)) # proper matrix & dimensions
plot_ly(x = x, y = y, z = z) %>% add_surface()
My Problem: The final result does not look similar to the result from the Wikipedia page:
Can someone please show me what I am doing wrong? Is there an easier way to do this?
Thanks!