I'm trying to determine the maximum revenue that can be earned from a battery connected to the grid using linear programming. The battery can earn revenues in two markets, the energy market and the frequency market. My model is throwing an error when I include a binary constraint in the objective function (TypeError: Non-constant expressions cannot be multiplied).
My Objective function is:
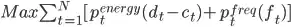
- N is the time horizon of the optimisation
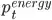 is the energy price at time t
is the energy price at time t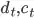 are the allocated discharge and charge power at time t
are the allocated discharge and charge power at time t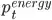 is the frequency price at time t
is the frequency price at time t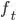 is the allocated frequency power at time t
is the allocated frequency power at time t
The battery should only be active in one market (energy or frequency) at each time period t. So needs a constraint that looks something like this:
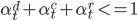
where 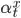 is a binary variable that activates activity x.
is a binary variable that activates activity x.
Ok, so that's what I trying to achieve. I'm struggling to create such a constraint in pulp that essentially switches off participation in one of the markets if the value in the other is higher (all other constraints being met). In my battery class, I've created decision variables for each of the power activities and also for their on/off status.
self.charge = \
pulp.LpVariable.dicts(
"charging_power",
('c_t_' + str(i) for i in range(0,time_horizon)),
lowBound=0, upBound=max_charge_power_capacity,
cat='Continuous')
self.discharge = \
pulp.LpVariable.dicts(
"discharging_power",
('d_t_' + str(i) for i in range(0,time_horizon)),
lowBound=0, upBound=max_discharge_power_capacity,
cat='Continuous')
self.freq = \
pulp.LpVariable.dicts(
"freq_power",
('f_t_' + str(i) for i in range(0,time_horizon)),
lowBound=0, upBound=max_freq_power_capacity,
cat='Continuous')
self.charge_status = \
pulp.LpVariable.dicts(
"charge_status",
('c_status_t_' + str(i) for i in range(0,time_horizon)),
cat='Binary')
self.discharge_status = \
pulp.LpVariable.dicts(
"discharge_status",
('d_status_t_' + str(i) for i in range(0,time_horizon)),
cat='Binary')
self.freq_status = \
pulp.LpVariable.dicts(
"freq_status",
('ds3_status_t_' + str(i) for i in range(0,time_horizon)),
cat='Binary')
In my objective function, I included these binary variables.
self.model = pulp.LpProblem("Max Profit", pulp.LpMaximize)
self.model +=\
pulp.lpSum(
[self.charge['c_t_' + str(i)]*-1*prices[i] *
self.charge_status['c_status_t_' + str(i)] for i in range(0,self.time_horizon)]
+ [self.discharge['d_t_' + str(i)]*prices[i] *
self.discharge_status['d_status_t_' + str(i)] for i in range(0,self.time_horizon)]
+ [self.freq['f_t_' + str(i)]*freq_prices[i] *
self.freq_status['freq_status_t_' + str(i)] for i in range(0,self.time_horizon)]
)
The constraint for these binary variables, I set up as follows:
for hour_of_sim in range(1,self.time_horizon+1):
self.model += \
pulp.lpSum([self.charge_status['c_status_t_' + str(i)] for i in range(0,self.time_horizon)] +\
[self.discharge_status['d_status_t_' + str(i)] for i in range(0,self.time_horizon)] +\
[self.freq_status['freq_status_t_' + str(i)] for i in range(0,self.time_horizon)]
) <= 1
When I try to solve, I get a
TypeError: Non-constant expressions cannot be multiplied
on the objective function. Doesn't like my binary variables, runs if they are removed. There must be an alternative way of setting this up which is escaping me?