Can't get the correct parameter fit for a system of ODEs using Symfit and some experimental results

Question

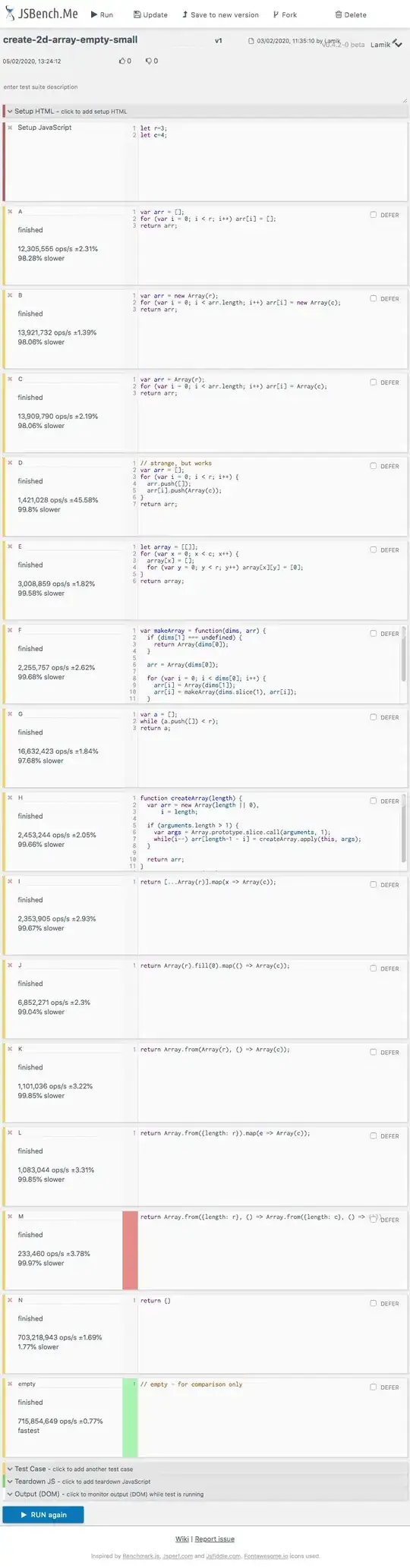
I want to fit the following model: To some fluorescence measurements ([YFP] over time). Basically I can measure the change of YFP over time, but not the change of x. After navigating through different solutions in overflow (and trying various of the solutions proposed), I finished getting pretty close with Symfit. However, when I try to fit the model to the experimental results, I get the following fit results:

Parameter Value        Standard Deviation
TauOFF    4.425923e-02 2.173698e+00
TauON     9.687891e+00 1.945774e+02
TauONx    4.539607e-02 2.239210e+00
x_SS      7.968579e+00 2.726591e+02
Status message         Maximum number of function evaluations has been exceeded.
Number of iterations   443
Objective              <symfit.core.objectives.LeastSquares object at 0x000002640701C898>
Minimizer              <symfit.core.minimizers.NelderMead object at 0x000002640701CEF0>

Goodness of fit qualifiers:
chi_squared            480161.4690600715
objective_value        240080.73453003576
r_squared              0.9677940481847731

I don't understand why X's prediction is so low, and almost a constant (almost because when I zoom in, it actually changes a little bit). Also, it says that "Maximum number of function evaluations has been exceeded". What am I doing wrong?? Am I am using the wrong minimizer? The wrong initial parameter estimated values?

Below is my code:

# %% Importing modules
import symfit
from symfit import parameters, variables, ODEModel, Fit, Parameter, D
from symfit.core.objectives import LogLikelihood
from symfit.core.minimizers import NelderMead
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sympy.solvers import ode

# %% Experimental data. Inputs is time, outputs is fluorescence measurements ([YFP])
inputs = np.array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17,
   18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
   35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
   52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66])
outputs = [73.64756293519015, 44.83500717360115, 66.59467242620596, 49.65998568360771, 46.484859217283514, 72.37530519707008, 74.47354904982025, 61.437468439656605, 80.15204098496119, 93.11740890688259, 74.73900664346728, 87.38835848475512, 94.96499329658872, 116.07910576096306, 126.95045168354777, 123.76237623762376, 147.73432650527624, 168.04489072652098, 183.3221551531411, 321.22186495176834, 356.38957816377166, 389.03440885819737, 321.22186495176834, 356.38957816377166, 389.03440885819737, 582.1501961516907, 607.139657798083, 651.6151143860851, 682.4329863103533, 716.422610612502, 749.3927432822223, 777.726234656009, 809.6079246328624, 847.2845376012857, 870.6370831711431, 895.512942218847, 914.3568311720239, 1002.7537605116663, 1019.3525890625908, 1028.7006485379452, 1073.162564875272, 1080.7277331278212, 1106.8392267287595, 1119.0425361584034, 1139.207233729366, 1145.790182270091, 1177.2867420349437, 1185.0114126299773, 1196.1818638533032, 1213.7383689107828, 1208.2922013820337, 1209.8943558642277, 1225.7463589296947, 1232.9657629893582, 1221.7722725107194, 1237.6858956142842, 1240.1111320399323, 1240.6384572177496, 1249.767333643555, 1247.0462864291337, 1259.6783113651027, 1258.188648128636, 1267.006026296567, 1272.2310666363428, 1260.6866757617101, 1266.8857660924748]

# %% Model Definitions
x, y, t = variables('x, y, t')
TauONx = Parameter('TauONx', 0.1)
TauON = Parameter('TauON', 0.180854297)
### For a moment, I thought of fixing TauOFF, obtaining this value from other experiments
TauOFF = Parameter('TauOFF', 10.53547354)
#TauOFF = 10.53547354
x_SS = Parameter('x_SS', 0.1)

#### All of this is using symfit package!
model_dict = {
    D(x, t): TauONx*(x_SS - x),
    D(y, t): TauON*x - TauOFF*y,
}
# %% Execute data
ode_model = ODEModel(model_dict, initial={t: 0.0, x: 54 * 10e-4, y: 54 * 10e-4})
    
fit = Fit(ode_model, t=inputs, x=None, y=outputs, minimizer=NelderMead)
#fit = Fit(ode_model, outputs, objective=LogLikelihood)
fit_result = fit.execute()
print(fit_result)

# %% Plot the data generated vs the output
tvec = np.linspace(0, 60, 1000)
X, Y = ode_model(t=tvec, **fit_result.params)
plt.plot(tvec, X, label='[x]')
plt.plot(tvec, Y, label='[y]')
plt.scatter(inputs, outputs)
plt.legend()
plt.show()

Your system is linear and thus relatively rigid. Thus when you fix the initial values this far away from the data at the initial point, you will get a bad fit. Set the initial values to also be variable during the fit. — Lutz Lehmann, Jan 07 '22 at 06:50
The parameters are redundant, a change in TauON can be compensated by a change in the scale of x and related changes in the parameters TauONx and x_SS of the x equation. — Lutz Lehmann, Jan 07 '22 at 16:47
Yes, you get convergence to the curve of equivalent parameters, but not necessarily to a specific point on it. Setting `x_SS=1000` gave a good fit in the `y` curve. You could also directly fit a second order DE with constant coefficients, which also has 3 parameters. I then get `[x0, y0] = [-674.18929763 254.97015568]`, `[TauONx, TauON, TauOFF] = [0.07163137 0.10354771 0.07162365]` — Lutz Lehmann, Jan 07 '22 at 18:01
Do you know how to set initial value estimates as variables using symfit? — Pedro Fontanarrosa, Jan 07 '22 at 18:10
Let us [continue this discussion in chat](https://chat.stackoverflow.com/rooms/240839/discussion-between-pedro-fontanarrosa-and-lutz-lehmann). — Pedro Fontanarrosa, Jan 07 '22 at 18:14
I was using scipy.optimize.curve_fit, this is rather basic, without the automatic report generation. — Lutz Lehmann, Jan 07 '22 at 18:16
These are the variable initial values. It is quite likely that especially the negative value for x is inappropriate. The curve of y also dips shortly into the negative range before curving back up. // I would try to declare them also as `Parameter` and pass them into the initial-condition dictionary. I do not know if this can work. — Lutz Lehmann, Jan 07 '22 at 20:53

Can't get the correct parameter fit for a system of ODEs using Symfit and some experimental results

0 Answers0