You have three points that are supposed to be on a Gaussian curve; this means that they lie on the function:
If you take the logarithm of this function, you get:

which is just a simple 2nd grade polynomial, i.e. a parabola with a vertical axis of simmetry:
with

So, if you know the three coefficients of the parabola, you can derive the parameters of the Gaussian curve; incidentally, the only parameter of the Gaussian function that is of some interest to you is b, since it tells you where the center of the distribution, i.e. where is its maximum. It's immediate to find out that

All that remains to do is to fit the parabola (with the "original" x and the logarithm of your values). Now, if you had more points, a polynomial fit would be involved, but, since you have just three points, the situation is really simple: there's one and only one parabola that goes through three points.
You now just have to write the equation of the parabola for each of your points and solve the system:

(with 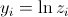 , where the zs are the actual values read at the corresponding x)
, where the zs are the actual values read at the corresponding x)
This can be solved by hand (with some time), with some CAS or... looking on StackOverflow :) ; the solution thus is:
So using these last equations (remember: the ys are the logarithm of your "real" values) and the other relations you can easily write a simple algebraic formula to get the parameter b of your Gaussian curve, i.e. its maximum.

(I may have done some mess in the calculations, double-check them before using the results, anyhow the procedure should be correct)
(thanks at http://www.codecogs.com/latex/eqneditor.php for the LaTeX equations)






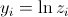 , where the zs are the actual values read at the corresponding x)
, where the zs are the actual values read at the corresponding x)
