Implement ball bouncing in free fall using scipy.ivp()

Question

I want to solve ordinary differential equations using scipy_ivp() of a ball falling with an inital velocity of 1 in the x-direction, and 0 in the y-direction. The gravitational acceleration is g = 9.82, and when the ball hits the ground, its velocity is suppossed to change sign and be multiplied by 0.9. However, using the events parameter, I find it doesn't work as it should. This is my code and the result:

from scipy.integrate import solve_ivp
def f_derivs_ivp(t, vars, g = 9.82):
    
    dxdt = vars[2]
    dydt = vars[3]
    
    dvxdt = 0
    dvydt = -g
    
    return dxdt, dydt, dvxdt, dvydt

def bounce(t, y, g = 9.82):
    if y[1] <= 0:
        y[3] = -0.9*y[3]
    #print(y[1])
    return y[1]

#bounce.terminal = True
#bounce.direction = -1

vars0 = np.array([0, 10, 1, 0])

sol = solve_ivp(f_derivs_ivp, [0, 7], vars0, max_step=0.01, events = bounce)


plt.plot(sol.y[0], sol.y[1], "ko")

print(sol.y_events)
print(sol.t_events)

Using another method than scipy.ivp(), the result should look like this:

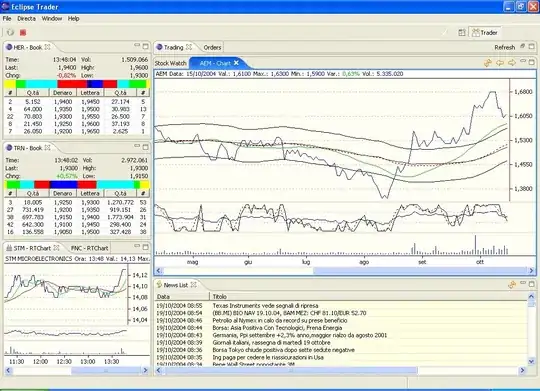
What am I doing wrong, and how does the events parameter work? Note also that if I write return y[1] - 10 in the bounce function, nothing changes. It bounces up and down if I in the if statement of the bounce function write y[3] = 10 for example, but not as it should.

score 3 · Accepted Answer · answered Dec 15 '21 at 21:09

The scipy ODE solvers do not possess an event-action mechanism with user-definable actions. The event function is just a scalar-valued function on the trajectory whose zeros (with crossing-direction if set) are the events. This means that the event function is used to search for an event (first detecting sign changes, then refining using Brent's method). It will be called multiple times per time step independent on if the time step contains an event.

The built-in actions are "register" (default) and "terminate".

You will have to interrupt the integration at a bounce, and restart with the reflected state as initial condition. Plot the pieces separately or use concatenation to get one big solution array.

Zor Ro · Answer 2 · 2023-08-07T11:49:06.923

You can use the event handler of solve_ivp indeed to detect the impact of the ball when hitting the ground by firing a termination of the simulation when y<=0.

After termination, safe all states of last time step, reduce velocity and reverse the y-direction (in your case -0.9). Then pass the array as initial condition for the next run. Loop until you reach the defined simulation end time. To exit the simulation loop completely, add a second event detection called "end_of_simulation". If tend - t < 0, the simulation gets terminated completely.

Notice, that the time vector as well as all state vectors need to be stacked together in each loop.

In addition, turn off velocity as well as gravity once the balls velocity is under a certain threshold (e.g., 0.1m/s). Otherwise, the ball will "fall" through the ground. Please let me know if somebody has a better idea to handle such case.

All in all it looks like this:

from scipy.integrate import solve_ivp
import numpy as np
from matplotlib import pyplot as plt


def falling_obj_rhs(t, Y, *args):
    
    g, _= args
    
    dxdt = Y[2,0]
    dydt = Y[3,0]
    
    dvxdt = 0
    dvydt = g
    
    return dxdt, dydt, dvxdt, dvydt

def hit_ground(t, Y, *args): 
    return Y[1]


def end_of_simulation(t, Y, *args):
    _, tend = args
    
    return tend - t
    

def main():

    g       = -9.81
    t_start = 0
    t_end   = 7
    
    # the function y is approaching the x axis from above --> negative slope
    hit_ground.direction       = -1  
    hit_ground.terminal        = True
    end_of_simulation.terminal = True
    
    #       x, y, vx, vy
    ic   = [0, 10, 1, 0]
    tsim = np.array([])
    ypos = np.array([])
    
    while t_start < t_end:
        
        sol = solve_ivp( falling_obj_rhs, 
                         [t_start, t_end], 
                         ic, 
                         method     = 'LSODA',
                         max_step   = 0.01, 
                         events     = [hit_ground, end_of_simulation], 
                         vectorized = True,
                         rtol       = 1e-6, 
                         atol       = 1e-9,
                         first_step = 1e-6,
                         args       = (g, t_end) )
        
        
        # store solution from last time step as initial condition
        ic = sol.y[:,-1]
        # reduce initial condition of y-velocity (energy loss du to collistion)
        # and change sign
        ic[-1] = ic[-1]*-0.9
        # turn off gravity and velocity once the ball is on the ground
        if sol.y[:,-1][-1] < 0.05:
            ic[-1] = 0
            g      = 0
        
        t_start = sol.t[-1]
        tsim = np.concatenate([tsim, sol.t[:]], axis=0)
        ypos = np.concatenate([ypos, sol.y[1]], axis=0)
    
    plt.plot(tsim, ypos, label='obj. trajectory')
    plt.xlabel('t')
    plt.ylabel('y')
    plt.grid()
    plt.legend()


if __name__ == '__main__':
    main()

Implement ball bouncing in free fall using scipy.ivp()

2 Answers2

Linked