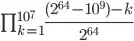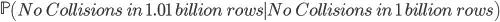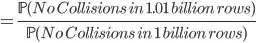1

I'm trying to understand the probability of collision of new hashes, given no collisions in the existing hash table yet.

For illustration, let's say I have a table where I store hashes of each row.

  1. The table currently has 1 billion rows
  2. There are no hash collisions amongst those 1 billion rows.
  3. I'm using a 64-bit hash algorithm.

Now imagine I insert 10 million new rows of data into the table. What is the probability that I have a hash collision now? I think the answer is the following:

Each new row's hash cannot have the same value of any of the existing rows or the new ones processed before itself. That removes 1 billion hash values from the 2^64 possibilities, so the probability of new collisions should be:

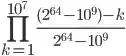
Does that sound right?

Chandler Sommerville
  • 33
  • 1
  • 5
  • 1
    Looks right to me. – RBarryYoung Nov 22 '21 at 17:05
  • Looks wrong to me. – President James K. Polk Nov 22 '21 at 23:39
  • 1
    I think you're right. The denominator should be 2^64, since there are still 2^64 possible hash values. And that gives the probability that we **do not** have a hash collision, not that we do have one. – Chandler Sommerville Nov 23 '21 at 13:00
  • Yes, that was my thinking. The prob of getting a collision at step k is p_k = (10^9+k)/2^64, so the prob of not getting one is 1-p_k. The prob of not getting a collision *after* T steps is q = prod(k=1 to T) [1-p_k], so the prob of getting a collision somewhere in those T steps is 1-q. But note: I get prob and stat problems wrong all the time, so don't trust me. – President James K. Polk Nov 23 '21 at 20:24

1 Answers1

0

Thanks to President James K. Polk, I realized that my original solution was wrong. The probability of no collisions is

Another way to think of it is just using the definition of conditional probability.

...which reduces to...

...which can be reduced to the product formula.

The benefit of the conditional probability formula is that it can be easily estimated using any of the online hash collision probability calculators.

Chandler Sommerville
  • 33
  • 1
  • 5