Because the weights are frequency weights, the most accurate method is to duplicate the observations according to the weights.
Adjusting the weights
Normally, frequencies are whole numbers. However, the frequencies here merely show how frequently an item appears relative to the other items of the same group. In this case, you can multiply all the weights by a value that makes the weights integers and use that value consistently throughout the dataset.
Here is a function that helps you choose the smallest possible set of weights to minimize memory usage and returns the weights as integers.
def adjust(weights):
base = 10 ** max([len(str(i).split(".")[1]) for i in weights])
scalar = base / np.gcd.reduce((weights * base).astype(int))
weights = weights * scalar
return weights
You can refer to the following question to understand how this function works.
df = pd.DataFrame({
"location": ["a", "a", "b", "b"],
"values": [1, 5, 3, 7],
"weights": [0.9, 0.1, 0.8, 0.2]
})
df.loc[:, "weights"] = adjust(df["weights"])
Here are the weights after the adjustment.
>>> df
location value weights
0 a 1 9.0
1 a 5 1.0
2 b 3 8.0
3 b 7 2.0
Duplicating the observations
After adjusting the weights, you need to duplicate the observations according to their weights.
df = df.loc[df.index.repeat(df["weights"])] \
.reset_index(drop=True).drop("weights", axis=1)
You can refer to the following answer to understand how this process works.
Let's count the number of observations after being duplicated.
>>> df.count()
location 20
values 20
Performing Statistical Operations
Now, you can use groupby and aggregate using any statistical operations. The data is now weighted.
df1 = df.groupby("location").agg(["median", "skew", "std"]).reset_index()
df2 = df.groupby("location").quantile([0.1, 0.9, 0.25, 0.75, 0.5]) \
.unstack(level=1).reset_index()
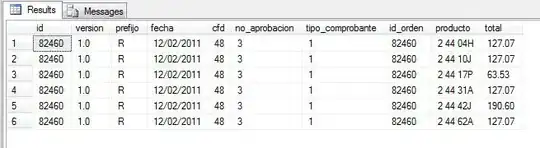
print(df1.merge(df2, how="left", on="location"))
This gives the following output.
location values
median skew std 0.1 0.9 0.25 0.75 0.5
0 a 1.0 3.162278 1.264911 1.0 1.4 1.0 1.0 1.0
1 b 3.0 1.778781 1.686548 3.0 7.0 3.0 3.0 3.0
Interpreting the weighted statistics
Let's follow the same process above but instead of giving the weights the smallest possible value, we will gradually duplicate the weights
and see the results. Because the weights are at their minimum values, the greater sets of weights will be the multiples of the current set. The following line will be changed.
df.loc[:, "weights"] = adjust(df["weights"])
adjust(df["weights"]) * 2
location values
median skew std 0.1 0.9 0.25 0.75 0.5
0 a 1.0 2.887939 1.231174 1.0 1.4 1.0 1.0 1.0
1 b 3.0 1.624466 1.641565 3.0 7.0 3.0 3.0 3.0
adjust(df["weights"]) * 3
location values
median skew std 0.1 0.9 0.25 0.75 0.5
0 a 1.0 2.80912 1.220514 1.0 1.4 1.0 1.0 1.0
1 b 3.0 1.58013 1.627352 3.0 7.0 3.0 3.0 3.0
adjust(df["weights"]) * 4
location values
median skew std 0.1 0.9 0.25 0.75 0.5
0 a 1.0 2.771708 1.215287 1.0 1.4 1.0 1.0 1.0
1 b 3.0 1.559086 1.620383 3.0 7.0 3.0 3.0 3.0
Repeat this process several times and we will get the following graph. The statistics in this graph are not split into groups and there are some other statistics added to it for demonstration purposes.
Some statistics like sample mean, median, and quantiles are always constant no matter how many times we duplicate the observations.
Some statistics, on the other hand, give different results depending on how many duplications we make. Let's call them inconsistent statistics for now.
There are two types of inconsistent statistics.
Inconsistent statistics that are independent of the sample size
For example: any statistical moments (mean, variance, standard deviation, skewness, kurtosis)
Independent here does not mean "not having the sample size in the equation". Notice how sample mean also has the sample size in its equation but it is still independent of the sample size.
For these types of statistics, you cannot compute the exact values because the answer may vary on different sample sizes. However, you can conclude, for example, the standard deviation of Group A is generally higher than the standard deviation of Group B.
Inconsistent statistics that are dependent on the sample size
For example: standard error of the mean and sum
Standard error, however, depends on the sample size. Let's have a look at its equation.
We can view standard error as the standard deviation per the square root of the sample size and therefore it is dependent on the sample size. Sum is also dependent on the sample size.
For these types of statistics, we cannot conclude anything because we are missing an important piece of information: the sample size.

