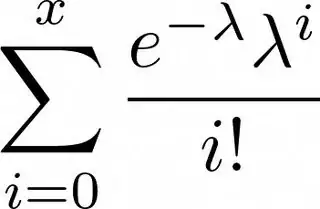Optimisation in Java Using Apache Commons Math

Question

I'm trying to minimise a value in Java usingcommons-math. I've had a look at their documentation but I don't really get how to implement it.

Basically, in my code below, I have a Double which has the expected goals in a soccer match and I'd like to optimise the probability value of under 3 goals occurring in a game to 0.5.


import org.apache.commons.math3.distribution.PoissonDistribution;

public class Solver {

    public static void main(String[] args) {

        final Double expectedGoals = 2.9d;
        final PoissonDistribution poissonGoals = new PoissonDistribution(expectedGoals);

        Double probabilityUnderThreeGoals = 0d;

        for (int score = 0; score < 15; score++) {
            final Double probability =
                    poissonGoals.probability(score);
            if (score < 3) {
                probabilityUnderThreeGoals = probabilityUnderThreeGoals + probability;
            }
        }

        System.out.println(probabilityUnderThreeGoals); //prints 0.44596319855718064, I want to optimise this to 0.5
    }
}

How about `expectedGoals = 2.67406` (if I understand correctly)? Also, note you can use `cumulativeProbability(2)` and don't need the loop. — Sweeper, Oct 27 '21 at 16:57
@Sweeper yes, 2.67406 is the correct value- but I was wondering how to implement the optimization algorithm for future cases when trial and error isn't so straightforward. — clattenburg cake, Oct 27 '21 at 17:03

Sweeper · Accepted Answer · 2021-10-27T18:37:47.030

The cumulative probability (<= x) of a Poisson random variable can be calculated by:

In your case, x is 2 and you want to find lambda (the mean) such that this is 0.5. You can type this into WolframAlpha and have it solve it for you. So rather than an optimisation problem, this is just a root-finding problem (though one could argue that optimisation problems are just finding roots.)

You can also do this with Apache Commons Maths, with one of the root finders.

int maximumGoals = 2;
double expectedProbability = 0.5;
UnivariateFunction f = x -> {
  double sum = 0;
  for (int i = 0; i <= maximumGoals; i++) {
    sum += Math.pow(x, i) / CombinatoricsUtils.factorialDouble(i);
  }
  return sum * Math.exp(-x) - expectedProbability;
};

// the four parameters that "solve" takes are:
// the number of iterations, the function to solve, min and max of the root
// I've put some somewhat sensible values as an example. Feel free to change them
double answer = new BisectionSolver().solve(Integer.MAX_VALUE, f, 0, maximumGoals / expectedProbability);
System.out.println("Solved: " + answer);
System.out.println("Cumulative Probability: " + new PoissonDistribution(answer).cumulativeProbability(maximumGoals));

This prints:

Solved: 2.674060344696045
Cumulative Probability: 0.4999999923623868

Optimisation in Java Using Apache Commons Math

1 Answers1