The background for my question is well explained in this SO question Is Dijkstra's algorithm deterministic?
Concretely, the answer by @Wyck illustrates the use-case I want to solve.
Image provided by @Wyck
My requirement is that boost's dijkstra_shortest_paths (based on the provided graph) when asked to produce a path from 0 to 5, always produces: 0->1->5, because the tie-breaking logic should use the lowest sum of the node IDs.
So, for lack of code, here's your sample codified with BGL:
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <boost/graph/graphviz.hpp>
struct VertexProps { };
struct EdgeProps { double weight = 1; };
using Graph = boost::adjacency_list<boost::vecS, boost::vecS, boost::directedS,
VertexProps, EdgeProps>;
using V = Graph::vertex_descriptor;
using E = Graph::edge_descriptor;
Graph make_graph();
int main() {
auto g = make_graph();
//write_graphviz(std::cout, g);
std::vector<V> predecessors(num_vertices(g));
boost::dijkstra_shortest_paths(g, 0,
boost::weight_map(get(&EdgeProps::weight, g))
.predecessor_map(predecessors.data()));
std::cout << "Path: ";
for (V v = 5; ; v = predecessors[v]) {
std::cout << " " << v;
if (v == predecessors[v])
break;
}
}
Graph make_graph() {
// sample from https://stackoverflow.com/questions/69649312/how-to-specify-tie-breaking-logic-in-boost-dijkstra-shortest-paths-dijkstra
Graph g;
add_edge(0, 1, g);
add_edge(0, 2, g);
add_edge(0, 3, g);
add_edge(0, 4, g);
add_edge(1, 5, g);
add_edge(2, 5, g);
add_edge(3, 5, g);
add_edge(4, 5, g);
return g;
}
Which prints
Path: 5 1 0
But if we reverse the order in which the edges are added:
Graph make_graph() {
Graph g;
add_edge(4, 5, g);
add_edge(3, 5, g);
add_edge(2, 5, g);
add_edge(1, 5, g);
add_edge(0, 4, g);
add_edge(0, 3, g);
add_edge(0, 2, g);
add_edge(0, 1, g);
return g;
}
It now prints Live
Path: 5 1 0
It seems that the graph model dictates the examination order. Let's fixate by using an ordered container selector (like setS) for edge storage:
using Graph = boost::adjacency_list<boost::setS, boost::vecS, boost::directedS,
VertexProps, EdgeProps>;
Now we can have a random insertion order:
#include <random>
#include <algorithm>
Graph make_graph() {
// sample from https://stackoverflow.com/questions/69649312/how-to-specify-tie-breaking-logic-in-boost-dijkstra-shortest-paths-dijkstra
using namespace std;
vector ee{pair{0, 1}, {0, 2}, {0, 3}, {0, 4},
{1, 5}, {2, 5}, {3, 5}, {4, 5}};
shuffle(ee.begin(), ee.end(), mt19937{random_device{}()});
Graph g;
for (auto [s, t] : ee)
add_edge(s, t, g);
return g;
}
And still always get (Live):
Path: 5 1 0
Code without tests is broken. Let's throw a wrench in the works:
Graph make_graph() {
vector ee{
tuple //
{0, 1, 1.0},
{0, 2, 1},
{0, 3, 1},
{0, 4, 1},
{1, 5, 2.0},
{2, 5, 1},
{3, 5, 1},
{4, 5, 1},
};
// shuffle(ee.begin(), ee.end(), mt19937{random_device{}()});
Graph g;
for (auto [s, t, w] : ee)
add_edge(s, t, EdgeProps{w}, g);
return g;
}
Note how we increased the weight for the 1 -> 5 edge alone. Now we get Live
Path: 5 4 0
Soooo... We expected 5 2 0 here. I decided to record an animation of the actual progress of the BFS search: Code On Coliru:¹
It becomes clear now that the intermediate queue favors later discoveries. We need to tweak the priority comparison.
Let's try to hack it with a custom Weight type instead of double:
struct Weight {
double magnitude = 0;
bool operator<(Weight const& rhs) const { return magnitude < rhs.magnitude; }
bool operator==(Weight const& rhs) const { return magnitude == rhs.magnitude; }
bool operator!=(Weight const& rhs) const { return magnitude != rhs.magnitude; }
Weight operator+(Weight const& rhs) const {
return {magnitude + rhs.magnitude};
}
friend std::ostream& operator<<(std::ostream& os, Weight const& w) {
return os << w.magnitude;
}
static Weight Inf() { return {std::numeric_limits<double>::infinity()}; }
};
Mutatis mutandis, this still works the same: Live On Coliru.
Of course, now the challenge becomes to include the "cumulative node ID sum" into the equation:
struct Weight {
double magnitude = 0;
size_t cumulative_node_id_sum = 0;
auto both() const { return std::tie(magnitude, cumulative_node_id_sum); }
bool operator<(Weight const& rhs) const { return both() < rhs.both(); }
bool operator==(Weight const& rhs) const { return both() == rhs.both(); }
bool operator!=(Weight const& rhs) const { return both() != rhs.both(); }
Weight operator+(Weight const& rhs) const {
return Weight{magnitude + rhs.magnitude,
cumulative_node_id_sum + rhs.cumulative_node_id_sum};
}
friend std::ostream& operator<<(std::ostream& os, Weight const& w) {
return os << w.magnitude;
}
static Weight Inf() {
return Weight{std::numeric_limits<double>::infinity(), 0};
}
};
Still the same (Live). Why? Because no initial weight actually knows the node id:
Let's initialize in make_graph:
for (auto e : boost::make_iterator_range(edges(g))) {
g[e].weight.cumulative_node_id_sum = target(e, g);
}
This sets the initial node ID sum to just the vertex ID for the target of each edge. With that in place, it all clicks:
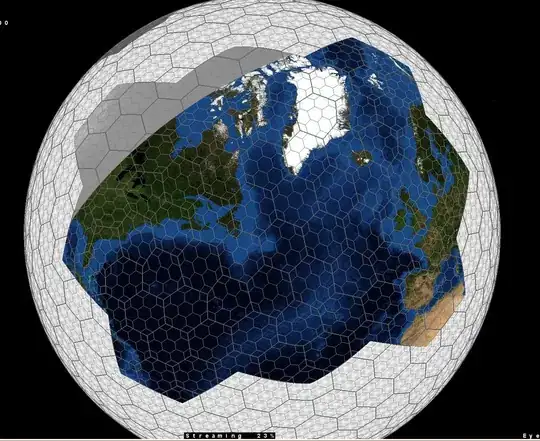
And indeed the path is back to the desired:
Path: 5 2 0
With that all understood, we can probably do lipo-suction on that diagnostic code. We sprinkle a tiny bit of magic so the default expression for distance_inf works:
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <iostream>
using namespace std::literals;
using Traits = boost::adjacency_list_traits<boost::setS, boost::vecS, boost::directedS>;
using V = Traits::vertex_descriptor;
using E = Traits::edge_descriptor;
struct Weight {
double magnitude = 0;
size_t cumulative_node_id_sum = 0;
Weight(double magnitude = 0, size_t cumulative_node_id_sum = 0)
: magnitude(magnitude)
, cumulative_node_id_sum(cumulative_node_id_sum)
{ }
private:
auto both() const { return std::tie(magnitude, cumulative_node_id_sum); }
public:
bool operator<(Weight const& rhs) const { return both() < rhs.both(); }
bool operator==(Weight const& rhs) const { return both() == rhs.both(); }
bool operator!=(Weight const& rhs) const { return both() != rhs.both(); }
Weight operator+(Weight const& rhs) const {
return Weight{magnitude + rhs.magnitude,
cumulative_node_id_sum + rhs.cumulative_node_id_sum};
}
};
namespace std {
template <> struct numeric_limits<Weight> : numeric_limits<double> {
};
} // namespace std
struct EdgeProps {
Weight weight;
};
using Graph = boost::adjacency_list<boost::setS, boost::vecS, boost::directedS,
boost::no_property, EdgeProps>;
Graph make_graph();
int main()
{
auto g = make_graph();
std::vector<V> predecessors(num_vertices(g));
boost::dijkstra_shortest_paths( //
g, 0,
boost::predecessor_map(predecessors.data())
.weight_map(get(&EdgeProps::weight, g)));
std::cout << "Path: ";
for (V v = 5;; v = predecessors[v]) {
std::cout << " " << v;
if (v == predecessors[v])
break;
}
std::cout << "\n";
}
#include <random>
#include <algorithm>
Graph make_graph()
{
// sample from
// https://stackoverflow.com/questions/69649312/how-to-specify-tie-breaking-logic-in-boost-dijkstra-shortest-paths-dijkstra
using namespace std;
vector ee{
tuple //
{0, 1, 1.0},
{0, 2, 1},
{0, 3, 1},
{0, 4, 1},
{1, 5, 2.0},
{2, 5, 1},
{3, 5, 1},
{4, 5, 1},
};
shuffle(ee.begin(), ee.end(), mt19937{random_device{}()});
Graph g;
for (auto [s, t, w] : ee)
add_edge(s, t, EdgeProps{w}, g);
for (auto e : boost::make_iterator_range(edges(g))) {
g[e].weight.cumulative_node_id_sum = target(e, g);
}
return g;
}
Printing the trusty
Path: 5 2 0
¹ images combined using gifsicle -l -O9 -k32 -d 100 frame{0..31}.gif > test.gif
