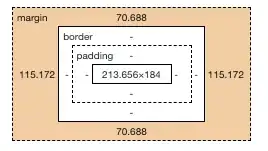
I'm trying to achieve the following image:

Where red is the ground truth circle (vehicle driving in a circle), and green is the Integration Drift (numerical errors that occur when integrating).
I started by plotting the circle and having difficulties plotting the integration drift with python.
Note: I'm trying to use scipy's integrate.cumtrapz instead of the multiplication in some places, but it doesn't help me.
These are the places I think it should be added and work:
psie = 0 + integrate.cumtrapz(psidote, t); # rad
xA1id = R0 + integrate.cumtrapz(0 + integrate.cumtrapz(xAddot1e, t), t); # m
xA2id = 0 + integrate.cumtrapz(R0*omega0 + integrate.cumtrapz(xAddot2e, t), t); # m
I believe the only issue in the code is in the variables xA1id and xA2id and up to that point, everything looks good.
The code I wrote is:
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
R0=5
omega0= np.pi
dt=0.001
N=1
te=np.arange(0,np.dot(2,N),dt)
psie=np.dot(omega0,te)
xA1e=np.dot(R0,np.cos(psie))
xA2e=np.dot(R0,np.sin(psie))
# circle plot
plt.plot(xA1e, xA2e, color='green', label='x-axis')
plt.show()
# Integration drift:
dt=0.01
N=100
t=np.arange(0,np.dot(2,N),dt)
# (1) Noise-free IMU "data":
psidote=np.dot(omega0,np.array([1]*len(t)))
a1e=np.dot((np.dot(- R0,omega0 ** 2)),np.array([1]*len(t)))
a2e=np.dot(0,a1e)
psie= t*psidote
xAddot1e=np.cos(psie)*a1e - np.sin(psie)*a2e
xAddot2e=np.sin(psie)*a1e +np.cos(psie)*a2e
xA1id=R0 + t* (t*xAddot1e)
xA2id= 0+t*((R0*omega0) + t* xAddot2e)
plt.plot(xA1id, xA2id, color='green', label='x-axis')
plt.show()
The equations come from: