Maxpooling 2x2 array only using numpy

Question

I want help in maxpooling using numpy. I am learning Python for data science, here I have to do maxpooling and average pooling for 2x2 matrix, the input can be 8x8 or more but I have to do maxpool for every 2x2 matrix. I have created an matrix by using

k = np.random.randint(1,64,64).reshape(8,8)

So hereby I will be getting 8x8 matrix as a random output. Form the result I want to do 2x2 max pooling. Thanks in advance

Answer 1

You don't have to compute the necessary strides yourself, you can just inject two auxiliary dimensions to create a 4d array that's a 2d collection of 2x2 block matrices, then take the elementwise maximum over the blocks:

import numpy as np

# use 2-by-3 size to prevent some subtle indexing errors
arr = np.random.randint(1, 64, 6*4).reshape(6, 4)

m, n = arr.shape
pooled = arr.reshape(m//2, 2, n//2, 2).max((1, 3))

An example instance of the above:

>>> arr
array([[40, 24, 61, 60],
       [ 8, 11, 27,  5],
       [17, 41,  7, 41],
       [44,  5, 47, 13],
       [31, 53, 40, 36],
       [31, 23, 39, 26]])

>>> pooled
array([[40, 61],
       [44, 47],
       [53, 40]])

---

For a completely general block pooling that doesn't assume 2-by-2 blocks:

import numpy as np

# again use coprime dimensions for debugging safety
block_size = (2, 3)
num_blocks = (7, 5)
arr_shape = np.array(block_size) * np.array(num_blocks)
numel = arr_shape.prod()
arr = np.random.randint(1, numel, numel).reshape(arr_shape)

m, n = arr.shape  # pretend we only have this
pooled = arr.reshape(m//block_size[0], block_size[0],
                     n//block_size[1], block_size[1]).max((1, 3))

Answer 2

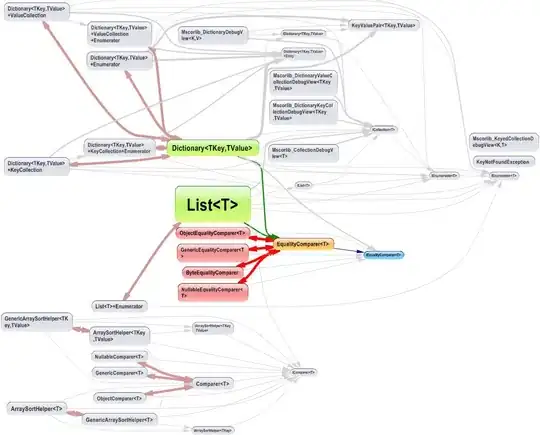
You can solve the convolution part using np.lib.stride_tricks which is actually how the numpy generates views from its methods in the background. Be careful though, this is memory level access to numpy arrays.

1. Convolve over the (8,8) matrix to get (4,4) matrices of (2,2) shape.
2. Reduce the (2,2) matrics with a pooling operation such as mean to get a (4,4) output.

This approach is scalable to larger matrices without any modification and can accommodate larger convolutions as well.

k = np.random.randint(1,64,64).reshape(8,8)

#Strides
x,y = 2,2

shape = k.shape[0]//x, k.shape[1]//y, x, y  
strides = k.strides[0]*x, k.strides[1]*y, k.strides[0], k.strides[1]

print('expected shape:',shape)
print('required strides:',strides)

convolve = np.lib.stride_tricks.as_strided(k, shape=shape, strides=strides)
print('convolution output shape:',convolve.shape)

maxpool = np.mean(convolve, axis=(-1,-2))
print('maxpooled output shape:',maxpool.shape)


print(' ')
print('Input matrix:')
print(k)
print('--------')
print('Output matrix:')
print(maxpool)

expected shape: (4, 4, 2, 2)
required strides: (128, 16, 64, 8)
convolution output shape: (4, 4, 2, 2)
maxpooled output shape: (4, 4)
 
Input matrix:
[[19 32 28 25 31 49 17 18]
 [ 4 19 50 57 29 42  5  8]
 [44 16 54 13 15  1 58 50]
 [18 36 29 12 39 45 47 44]
 [34 31 17 28 35 62 30 54]
 [38 50 14 50 25 24 36  4]
 [58 27 20 34 55 22 63 59]
 [61 30 37 24 23 34  5 16]]
--------
Output matrix:
[[18.5  40.   37.75 12.  ]
 [28.5  27.   25.   49.75]
 [38.25 27.25 36.5  31.  ]
 [44.   28.75 33.5  35.75]]

Just to confirm, if you take just the first (2,2) window of your matrix and apply mean pooling on it, you get 18.5 which is the first value of your output matrix, as expected.

first_window = [[19,32],
                 [4,19]]

np.mean(first_window)

# 18.5

---

EXPLANATION

Numpy stores its ndarrays as contiguous blocks of memory. Each element is stored in a sequential manner every n bytes after the previous.

So if your 3D array looks like this -

np.arange(0,16).reshape(2,2,4)

#array([[[ 0,  1,  2,  3],
#        [ 4,  5,  6,  7]],
#
#       [[ 8,  9, 10, 11],
#        [12, 13, 14, 15]]])

Then in memory its stores as -

When retrieving an element (or a block of elements), NumPy calculates how many strides (of 8 bytes each) it needs to traverse to get the next element in that direction/axis. So, for the above example, for axis=2 it has to traverse 8 bytes (depending on the datatype) but for axis=1 it has to traverse 8*4 bytes, and axis=0 it needs 8*8 bytes.

This is where arr.strides comes in. It shows the number of bytes required to access the next element in that direction.

For your case with the (8,8) matrix -

1. You want to convolve the 8x8 matrix by a (2,2) step in each direction, therefore resulting in a (4,4,2,2) shaped matrix. Then you want to reduce the last 2 dimensions in your maxpooling step with an average resulting in a (4,4) matrix.

2. The shape is what you define as your expected shape which is (4,4,2,2) in this case

3. The convolution needs to access memory however by take 2 steps in each direction (k.strides[0]*2 = 128 bytes and k.strides1*2 = 16 bytes to get the first element of the (2,2) window, then for another (64,8) bytes.

NOTE: The try to NEVER hardcode the strides/shapes in this function. Can result in memory issue. Always use calculate the expected strides and shape from the strides and shapes of the original matrix.

Hope this helps. Read more about stride_tricks here and here.