Dijkstra's bi-directional implementation

Question

I am implementing a bidirectional Dijkstra's algorithm and having issues understanding how the various implementations of the stopping condition work out.

Take this graph for example, where we're starting from node A, targetting node J. Below the graph I have listed the cluster (processed) and relaxed (fringes) nodes at the time the algorithm stops:

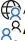
The accepted answer to “Bidirectional Dijkstra” by NetworkX explains that the algorithm stops when the same node has been processed in both directions. In my graph that will be Node F. If that were the case, the algorithm stops after finding the shortest path of length 9 going from A-B-C...H-I-J. But this wouldn't be the shortest path because A-J have a direct edge of length 8 which is never taken because the weight 8 is never popped from the priority queue.

Even in this Java implementation on github of Dijksta's bi-directional algorithm, the stopping condition is:

double mtmp = DISTANCEA.get(OPENA.min()) +
                          DISTANCEB.get(OPENB.min());            
if (mtmp >= bestPathLength) return PATH;

This algorithm stops when the top node weights -- from each front and backward queue -- add up to at least the best path length so far. But this wouldn't return the correct shortest path either. Because in that case it will be node G(6) and E(5) totalling to 11, which is greater than the best path so far of length 9.

I don't understand that seemingly both of these stopping conditions yield an incorrect shortest path. I am not sure what I am misunderstanding.

What is a good stopping condition for Dijkstra's bidirectional algorithm? Also, what would be a stopping condition for bidirectional A*?

Answer 1

Conceptually the stopping condition for Dijkstra's algorithm, whether bidirectional or not, is that you stop when the best path you've found is as good as any path you might find if you continue. Only closed paths (the ones in your "cluster" sets above) count as found.

For bidirectional Dijkstra's, a path is "found" whenever the same vertex exists in both the forward and reverse closed sets. That part is easy, but how good is the best path you might find in the future?

To make sure the answer you get is correct, you evaluation of the best path you might find needs to be accurate, or an underestimate. Lets consider the possibilities:

1. A path might be made with a vertex that is open in both directions.
2. A vertex that is open in one direction might make a path with one that is already closed in the other direction.

The problem is case (2). The sets and priority queues we use for Dijkstra's algorithm do not allow us to make a very useful underestimate of the best path in this case. The smallest distance in a closed set is always 0, and if we add this to the minimum open from the other direction, then we come up with:

double mtmp = min ( DISTANCEA.get(OPENA.min()) , DISTANCEB.get(OPENB.min()) );

This works, and will produce the correct answer, but it will make the algorithm run until the best complete path is found in at least one direction. Unidirectional Dijkstra's would be faster in many cases.

I think this "bidirectonal Dijkstra's" idea needs significant rework in order to be really good.