I have a coupled set of equations where the main PDE (function of time and position z) is given as:
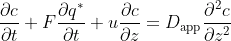
The second equation is of the type:
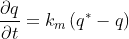
where k_m = f(q) and q^* = f(c). As you can see the second equation is an ODE (no dependence of q on space directly). I am finding it hard to write the code to couple the two equations. As of now for a simplistic case where I neglect the second equation and take: q = A*c, where A is some constant, I was able to simplify and just solve for the following convection diffusion equation:
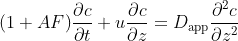
with the following code:
from fipy import Variable, FaceVariable, CellVariable, Grid1D, ExplicitDiffusionTerm, TransientTerm, DiffusionTerm, Viewer, AdvectionTerm, PowerLawConvectionTerm, VanLeerConvectionTerm
from fipy.tools import numerix
#define the grid
L = 3.
nx = L * 512
dx = L/nx
mesh = Grid1D(dx=dx, nx=nx)
# create the variable and initiate it's value on the mesh
conc = CellVariable(name="Conc", mesh=mesh, value=0.)
# physical parameters
Dapp = 1e-7
u = 0.1
A = 0.85
e = 0.4
F = (1-e)/e
# provide the simplified coefficients
DiffCoeff = Dapp/(1+A*F)
ConvCoeff = ((u/(1+A*F)),)
#Boundary conditions
valueLeft = 1
valueRight = 0.
conc.constrain(valueLeft, mesh.facesLeft)
conc.faceGrad.constrain(valueRight, where=mesh.facesRight)
# define the equation
eqX = TransientTerm() == (DiffusionTerm(coeff=DiffCoeff) - VanLeerConvectionTerm(coeff=ConvCoeff))
# time stepping parameters
timeStepDuration = 0.001
steps = 50000
from tqdm import tqdm
for step in tqdm(range(steps), desc="Iterating..."):
eqX.solve(var=conc,dt=timeStepDuration)
# plot every 5000 iterations
if step%5000 == 0:
viewer.plot()
Can someone help in coupling the convection diffusion equation with the ODE in the fipy framework. I am bit confused about how to take the right hand side which in the Finite Volume sense should be just a source term.
(https://www.codecogs.com/latex/eqneditor.php for generating the Latex equations)