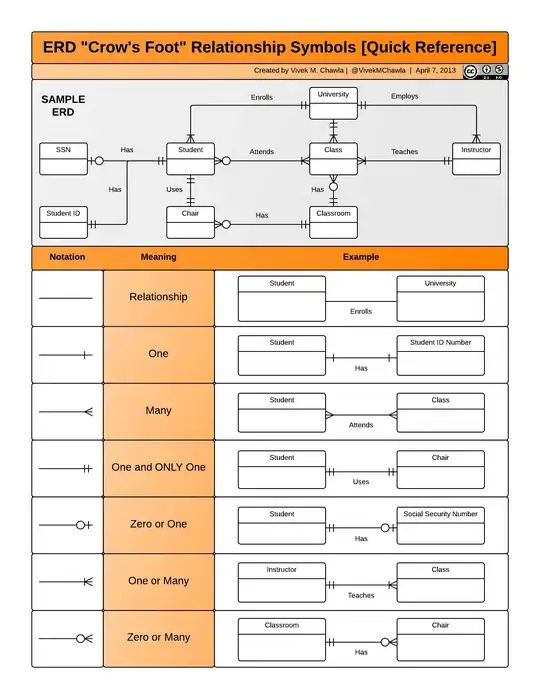
I'm new to survival analysis and quickly coded a baseline survival function with Python's Lifeline. But the graphs I get are too optimistic compared to the retention curves I plotted myself based on my data.
Below is a graph I made based on my data. It shows how many weeks clients from different cohorts stay. It is clear that people from Belgium (red line) stay longer than people from The Netherlands. After 20 weeks, 56% of Belgian customers are still there, while there are only 43% of the Dutchman.
But when I use Python's lifeline CoxPHFitter to plot the survival function, I get the graphs below:
It shows that the probability of "being alive" after 20 weeks is more than 70% for Belgian people and more than 50% for dutchman.
Why are these numbers different? Did I misinterpreted one of the curves?
This is my code:
cph = CoxPHFitter()
cph.fit(dumies, 'weeks_subscribed', event_col='stopped')
cph.plot_partial_effects_on_outcome('addresses__address__country__name_Nederland',values=[0,1])
Where 'stopped' is set to 1 if the customer isn't subscribed anymore. The average length of 'weeks_subscribed' is 18.
EDIT:
The way I calculated the retention graph manually is as follows:
def add_time_subscribed(rd):
rd['weeks_subscribed'] = 0
for index, row in rd.iterrows():
if (not row['stopped']) and (not row['_paused']):
end_date = datetime.now(tz=pytz.UTC)
else:
end_date = row['paused_at']
rd.loc[index,'weeks_subscribed'] = (end_date - row['subscribed_at']).days/7
def stayers_per_week(rd):
y_axis = np.zeros(int(rd['weeks_subscribed'].max())+1)
for index, row in rd.iterrows():
for i in range(int(row['weeks_subscribed'])+1):
y_axis[i] += 1
x_axis = [i for i in range(len(y_axis))]
return x_axis, y_axis/y_axis[0]