I imagine you're looking for some elegant method, but for now here's how to brute-force it:
Clear[findx];findx[d_,g_,b_]:=x/.First@FindRoot[x\[Equal]((b x+1)/(x+g))^d,{x,0,1},PrecisionGoal\[Rule]3]
ClearAll[plotQ];
plotQ[d_,g_,b_,eps_]:=Module[
{x=findx[d,g,b]},
Abs[(1-b g) x d/((b x+1) (x+g))-1.]<eps]
tbl=Table[{d,g,plotQ[d,g,.1,.001]},{d,4,20,.05},{g,1,1.12,.001}];
(this should take of the order of 10s). Then draw the points as follows:
Reap[
Scan[
If[#[[3]] == True,
Sow@Point[{#[[1]], #[[2]]}]] &,
Flatten[tbl, 1]]] // Last // Last //
Graphics[#, PlotRange -> {{1, 20}, {1, 1.1}}, Axes -> True,
AspectRatio -> 1, AxesLabel -> {"d", "g"}] &
Painfully ugly way to go about it, but there it is.
Note that I just quickly wrote this up so I make no guarantees it's correct!
EDIT: Here is how to do it with only providing b and a stepsize for d:
Clear[findx];
findx[d_, g_, b_] :=
x /. First@
FindRoot[x \[Equal] ((b x + 1)/(x + g))^d, {x, 0, 1},
PrecisionGoal \[Rule] 3]
ClearAll[plotQ];
plotQ[d_, g_, b_, eps_] :=
Module[{x = findx[d, g, b]},
Abs[(1 - b g) x d/((b x + 1) (x + g)) - 1.] < eps]
tbl = Table[{d, g, plotQ[d, g, .1, .001]}, {d, 4, 20, .05}, {g, 1,
1.12, .001}];
ClearAll[tmpfn];
tmpfn[d_?NumericQ, g_?NumericQ, b_?NumericQ] :=
With[{x = findx[d, g, b]},
(1 - b g) x d/((b x + 1) (x + g)) - 1.
]
then
stepsize=.1
(tbl3=Table[
{d,g/.FindRoot[tmpfn[d,g,.1]\[Equal]0.,
{g,1,2.},PrecisionGoal\[Rule]2]},
{d,1.1,20.,stepsize}]);//Quiet//Timing
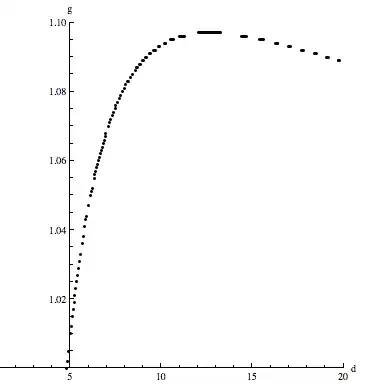
ListPlot[tbl3,AxesLabel\[Rule]{"d","g"}]
giving