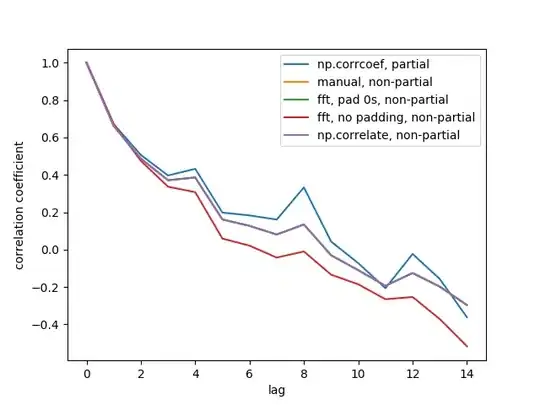
OK I have come up with an example solution.
To break it into the three parts:
- Identify a vector of coordinates for a contour line for Z that intersects with the sample site;
- Identify a vector of coordinates for a gradient line (line of maximum slope) for Z that intersects with the sample site;
- Calculate the distance along the focal site's contour line from the focal site to the intersecting gradient line for each other sample site (not the straight-line distance)
Sample data
For this example I use the inbuilt volcano data. See ?volcano for details. I'm still getting my head around spatial data in R, so forgive me for jumping between sf and terra (and sometimes raster) throughout the example.
library(terra)
library(tidyverse)
library(sf)
# sample raster data
v <- rast(volcano)
# manually assign a crs and extent to the volcano data - we need a crs to calculate distance, later on
# this is not meant to be spatially perfect, but is done to demonstrate this example - see ?volcano; grid cells are 10x10 m, hence the manual extent assignment
crs(v) <- '+proj=utm'
ext(v) <- ext(0, 610, 0, 870)
plot(v)
# choose two example sites
lon <- c(244, 427)
lat <- c(174, 713)
lonlat <- cbind(lon, lat)
sites <- vect(lonlat, crs = '+proj=utm') # assign a crs matching the volcano data
# also make this into an 'sf' object - and add in site_id column
sites %>%
st_as_sf %>%
mutate(
site_id = row_number()
) %>%
{. ->> sites_sf} %>%
# and also turn back into SpatVector, now with site_id
vect %>%
{. ->> sites_vect}
# plot raster and sites
plot(v)
points(sites_vect)

1 - Identify contour line passing through sample site
So, I chose site 2 (coords 427,713) as the one to get the contour line for. This is pretty straightforward using terra::extract to get site elevations, and then terra::as.contour to get contour lines of your chosen elevation.
# step 1 - find contour line of a site
# example, find contour line of site 2 [427,713]
# isolate site 2
sites_sf %>%
filter(
site_id == 2
) %>%
{. ->> site_2_sf}
# find elevation of the site
terra::extract(v, sites_vect) %>%
{. ->> site_elevations}
site_elevations
# ID lyr.1
# 1 134
# 2 165
# get the contour lines of the sample site's elevation (there is 2 lines)
v %>%
terra::as.contour(levels = site_elevations[2,2]) %>%
{. ->> contours} %>%
st_as_sf %>%
{. ->> contours_sf_1} %>% # also save it as an sf object
plot(add = TRUE)
# this is a sf collection - of a single MULTILINESTRING
So now we have the contour lines as a single MULTILINESTRING. We want to split these into two separate LINESTRINGs so we can subset and keep only the one that intersects the sample site. We use st_cast('LINESTRING') to split the MULTILINESTRING into separate LINESTRINGs.
# first, we split the MULTILINESTRING into 2 individual LINESTRINGs
contours_sf_1 %>%
st_cast('LINESTRING') %>%
mutate(
line_id = row_number()
) %>%
{. ->> contours_sf_2}
# find which LINESTRING intersects sample site 2
contours_sf_2 %>%
filter(
# st_intersects(contours_sf_2, sites_sf %>% st_buffer(0.1), sparse = FALSE)[1,]
st_intersects(contours_sf_2, site_2_sf %>% st_buffer(10), sparse = FALSE) # set a buffer width of 10 m, to ensure the line crosses the site
) %>%
{. ->> intersecting_contour}
intersecting_contour %>%
plot(col = 'red', add = TRUE)
# and we also rasterize it to use later
# (cells crossing the line have values of 1, other cells are NA)
intersecting_contour %>%
vect %>%
{. ->> intersecting_contour_vect} %>%
rasterize(., v) %>%
{. ->> intersecting_contour_rast}
Awesome, now we have isolated the (red) contour line which passes through the sample site.
2 - Identify line of maximum gradient from another sample site to the contour line
This is where it get's a bit more complex, but it is by no means a 'black box'. Here, I am using my own homemade function drain_f8.1() which I have modified from another function which I use to find drainage lines from (LIDAR-derived) elevation models, to find stream paths. I was going to include an earlier, simpler version of the function but every change I have made has been an improvement or correction on earlier versions, so here it is.
Basically, what drain_f8.1() does is:
- Uses
raster::getValuesFocal to find the values of the cells in a given cell's neighbourhood (default size of 3x3, or immediate neighbourhood).
- The maximum value in the neighbourhood is selected, and then using a
while() loop, the function steps to this cell next.
- In the event of duplicate maximums in the neighbourhood, the one with the lowest cell number in the neighbourhood (numbers left to right, top to bottom, like
raster cells are numbered) is chosen, unless the original cell also contains the max value.
- If no value greater than the original cell is located in the neighbourhood, then the size of the neighbourhood is increased by 1 cell in every direction, until
- a value larger than the original cell is found, in which case it steps there and proceeds as above
- the maximum neighbourhood area is searched (default 1000x1000 cells - this is massive but ensures the
while() loop stops eventually)
- or especially for this example, the function reaches a specified elevation
- the function then returns a
SpatVector which follows the line of maximum (uphill) gradient through the landscape, from the starting position to your contour line
I originally used this function to find minimum neighbourhood values, and maximum downhill gradient, so there may be relic comments in there referring to this concept. I came up with this function as an alternative to raster::flowPath, which terminates rather than searching a larger neighbourhood if it can't find a smaller value than the cell in question.
While the function is running, it prints the current iteration (cell) number, and neighbourhood search size in the console - this is handy so you know it is still going. If you add show_plot = TRUE it plots a point on a map as it finds the path and if you add testing = TRUE it adds Sys.sleep(0.5) in every loop so it goes a little slower and you can watch the plot or iterations closer. These both slow it down a little (insignificant in this example), but are handy for troubleshooting.
drain_f8.1 <- function(dem, x, y, ngb_size = 3, max_ngb = 1000, show_plot = FALSE, max_elev, testing = FALSE){
#----- version info -----
#* drain_f8.1()
#* CHANGES
#* - changed find_min() to find_max()
#* - included a max_elev input, so the line terminates when it gets to the desired elevation (and contour line)
#* - added a 'testing' input, which if TRUE delays each iteration of the loops by 0.5 seconds so you can watch the plotting and iteration progress
#* - if the current cell value is also the max in the neighbourhood, then the termination code is prioritised to induce a larger neighbourhood search area, rather than favouring lower cell numbers (top right direction)
#*
#*
#* drain_f8()
#* CHANGES
#* - added in (x, y) coordinate input instead of cell number input
#* - changed output to sf POINT collection
#*
#* CURRENT BUGS
#* - so it doesn't actually plot every point as it's added to the data, this needs to be investigated - FIXED so it does
#*
#* YET TO COME
#* - dem needs a decent buffer (like 100 m or more) - this is the reason for the stalling and neighbourhood size of 200 m at pond creek
#* - this depends on the dem we feed the function, not the function itself
#* - do we really need a while() loop inside the while() loop?
#* - I think this is why we don't see neighbourhood search sizes of 3 m in the progress report, when we should (actually this was the position of the print progress report - fixed)
#* - braided stream paths (currently we are only taking the first path, but we want braids if we can)
#*
#* KNOWN LIMITATIONS
#* - we just keep searching until there is a smaller value that a given cell, and then go straight to it
#* in an extreme example, say there is a hill with flat around it and a hole on the other side of out start cell
#* we would go straight through (over) the hill to the hole, rather than around it following the flat contour
#* water would instead flow over the flat contour (the minimum in the neighbourhood, aside from the start cell)
#* - based on our type of data (steep upland streams), and the resolution of the dems (1 m horizontal, centimetre vertical),
#* I don't think this is a big deal for us now, as we don't have the flat plains like described in the example
#* additionally, distance between points will be considered in gradient scrunity
#* drain_f7()
#* - add in the line drawing to the plot while it loops
#* drain_f6()
#* - this is the one where we will up the neighbourhood size if it terminates
#* drain_f5()
#* - include the neighborhood size in the final output
#* drain_f4()
#* - we've got a progress indicator now
#* drain_f3()
#* copy of drain_f2()
#* However
#* - we now get the cell coordinates as an export too
#* drain_f2()
#* so this is a copy of drain_f1
#* Inputs:
#* - dem
#* - start cell
#* - neighborhood size
#* Outputs:
#* - tibble of the drainage path
#----- sample data -----
# # ## sample data
# dem <- v # this is the elevation model/raster
# x <- 0.4 # starting coordinates of the gradient line (so this is the site not on the contour line)
# y <- 0.2
# ngb_size <- 3 # default neighbourhood size
# max_ngb <- 1000 # default maximum neighbourhood size to search
# show_plot <- TRUE # do we want to show the plot while the function works? (default = FALSE)
# max_elev <- 165 # once we achieve this elevation, we want the function and gradient line to terminate, and return the line it's found
# testing <- TRUE
#----- determine start_cell from coords -----
# cellFromXY needs to be supplied a matrix of the x and y coords
tibble(
x = x,
y = y
) %>%
as.matrix %>%
cellFromXY(dem, .) %>%
{. ->> start_cell}
#----- define find_max() function -----
# the find_max() function finds the maximum value
# and cell number in the neighbourhood of a given cell
# # testing value for duplicte maximums
# start_cell <- 3986
find_max <- function(dem, start_cell, ngb_size){
# we need to know the number of cells in the neighborhood
ngb_squ <- ngb_size^2
# find row number of start cell
dem %>%
rowFromCell(start_cell) %>%
{. ->> start_row}
# find col number of start cell
dem %>%
colFromCell(start_cell) %>%
{. ->> start_col}
# we make a tibble for position codes and their relative positions
# position 1 is the top left of the neighbourhood, and numbers increase left to right
# and down the rows, just like a Raster does
tibble(
pos = 1:ngb_squ
) %>%
mutate(
row = ceiling(pos/ngb_size),
col = rep(1:ngb_size, ngb_size),
rel_row = row - median(row),
rel_col = col - median(col)
) %>%
{. ->> pos_codes}
# find the max value in the start cell's neighborhood
# use raster::getValuesFocal() to find the values in the neighborhood
dem %>%
raster::raster() %>%
raster::getValuesFocal(row = start_row, nrows = 1, ngb = ngb_size, names = FALSE) %>%
# keep only the cell column we want (which is row number in this case)
as_tibble %>%
filter(
row_number() == start_col
) %>%
# make long format
pivot_longer(1:ngb_squ) %>%
# detemrine position codes for each cell
mutate(
pos = as.numeric(str_replace(name, 'V', ''))
) %>%
# join in our position codes and relative positions
left_join(pos_codes, by = 'pos') %>%
# keep the maximum value
filter(
value == max(value, na.rm = TRUE)
) %>%
# determine cell number from relative position
mutate(
cell_row = start_row + rel_row,
cell_col = start_col + rel_col,
cell_2 = cellFromRowCol(dem, cell_row, cell_col),
cell_1 = start_cell,
cell_2_value = value,
terminate = ifelse(cell_2 == cell_1, 1, 0),
ngb_size = ngb_size
) %>%
# dplyr::select(cell_number, cell_value, prev_cell, terminate) %>%
dplyr::select(cell_1, cell_2, cell_2_value, terminate, ngb_size) %>%
# new - if the cell value is also the maximum in the neighbourhood, we prioritise the termination code to the top of the tibble
# to induce a larger neighbourhood search area
# rather than (previously) favouring the cell with the lowest position number (favouring the top right)
arrange(desc(terminate)) %>%
# here, for now we only take the first cell, when there is a duplicate
filter(
row_number() == 1
)
}
#----- while() loop through find_max() -----
#* so, now we loop through find_max()
#* so this finds the max value in the neighbourhood, then moves to it
#* then, using the new cell, find the max value in it's neighbourhood
#* and so on
#*
#* the while() element allows it to search a larger
#* neighbourhood for a max value, larger than itself
#* in the case of multiple equal maximum values, the function
#* selects the first to appear, or the lowest position number
#* *ideally, this will be updated in the future to allow for river braiding and multiple paths
# so, first thing we do is find the maximum value in the start_cell's neighbourhood
find_max(dem, start_cell, ngb_size) %>%
{. ->> int_1}
# int_1
# set int_2 to nothing (in case we have a leftover)
int_2 <- NULL
#* if we are printing the plot as we go, this is where we print the dem
#* - points get printed after each while() iteration below
if(show_plot == TRUE){
plot(dem)
}
# so, we run the loop while we haven't hit a termination code, or hit the max_elev
while(last(int_1$terminate) == 0 & last(int_1$cell_2_value < max_elev)){
# while(last(int_1$terminate) == 0){
while(last(int_1$terminate) == 0 & last(int_1$cell_2_value < max_elev)){
if(testing == TRUE){
# for testing only - so you can watch the plotting and iteration count
Sys.sleep(0.5)
}
# if we are plotting as we go, add a point to the plot
if(show_plot == TRUE){
xyFromCell(dem, int_1[[nrow(int_1), 2]]) %>%
points
}
# take the current int_1 tibble, grab the last cell number, and run find_min() again
bind_rows(
int_1,
find_max(dem, last(int_1$cell_2), ngb_size)
) %>%
{. ->> int_1}
# and this prints the current progress (the main iteration progress)
if(last(int_1$terminate) == 0){
cat(paste0('\rcurrent iteration: ', str_pad(nrow(int_1), 5, side = 'left', pad = '0'), ', neighbourhood search size: ', str_pad(last(int_1$ngb_size), 3, side = 'left', pad = '0')))
}
}
int_1 %>%
tail(1) %>%
{. ->> int_2}
# so, while we have a termination, keep upping the neighbourhood size until we hit the max
while(last(int_2$terminate) == 1 & last(int_2$ngb_size <= max_ngb)){
if(testing == TRUE){
# for testing only - so you can watch the plotting and iteration count
Sys.sleep(0.5)
}
# this finds the max in a bigger neighbourhood
bind_rows(
int_2,
find_max(dem, last(int_1$cell_2), last(int_2$ngb_size) + 2)
) %>%
{. ->> int_2}
#* and this prints the current progress (the neighbourhood search progress)
#* - unlike other printings, this happens irrespective of termination codes
cat(paste0('\rcurrent iteration: ', str_pad(nrow(int_1), 5, side = 'left', pad = '0'), ', neighbourhood search size: ', str_pad(last(int_2$ngb_size), 3, side = 'left', pad = '0')))
}
#* now we join int_1 and int_2 together
#* so we have our new un-terminated cell at the tail
bind_rows(
int_1,
int_2 %>% tail(1)
) %>%
{. ->> int_1}
# and this prints the current progress
if(last(int_1$terminate) == 0){
cat(paste0('\rcurrent iteration: ', str_pad(nrow(int_1), 5, side = 'left', pad = '0'), ', neighbourhood search size: ', str_pad(last(int_1$ngb_size), 3, side = 'left', pad = '0')))
}
# this prints the final progress report, with a linebreak after it so it looks neat
if(last(int_1$terminate) == 1){
cat(paste('\riteration', nrow(int_1), '\n'))
}
}
# int_1
#----- find cell coords, convert to vect -----
#* now we find the coordinates of the cells in the final data
#* this is so we have a SpatVector
int_1 %>%
pull(cell_2) %>%
xyFromCell(dem, .) %>%
vect(type = 'lines')
}
So, we just need to supply drain_f8.1() with: raster data, coordinates of the sample site from which we are finding the max gradient line, and the elevation of the contour line where we want it to stop.
So, we grab the coordinates of site 1
# coords of site 1
sites_sf %>%
filter(
site_id == 1
) %>%
st_coordinates %>%
{. ->> site_1_coords}
And the elevation of site 2, and the contour line
# and our max elevation is the elevation of site 2
site_elevations[2,2]
And punch these into drain_f8.1()
# now we run the function, finding the line of maximum gradient until we reach the specified elevation (contour level)
drain_f8.1(dem = v, x = site_1_coords[1], y = site_1_coords[2], max_elev = site_elevations[2,2]) %>%
{. ->> max_gradient_line}
plot(v)
plot(sites, add = TRUE)
plot(intersecting_contour, add = TRUE)
plot(max_gradient_line, add = TRUE)
So now we just need to find distances along the contour line, and the maximum gradient line.
3.1 - Calculate distance along contour line to intersecting gradient line
I wasn't 100% sure if you wanted distance between sites or just distance to the gradient line, so I have examples of both - they are almost identical anyway. First we find distance to the line of max gradient, along the contour line.
# duplicate the contour line and gradient line
intersecting_contour_rast_3.1 <- intersecting_contour_rast
intersecting_contour_vect_3.1 <- intersecting_contour_vect
# plot the raster and the lines we have
v %>% plot
intersecting_contour_vect_3.1 %>% plot(add = TRUE)
max_gradient_line %>% plot(add = TRUE)
# ok, where do the 2 lines meet?
terra::intersect(intersecting_contour_vect_3.1, max_gradient_line) %>%
{. ->> point_1}
# plot the point of intersection
point_1 %>% plot(col = 'red', add = TRUE)
Now, we can use raster::gridDistance to find the distance between cells and an origin, ensuring the path follows cells of a certain value using omit. Here, we have a raster version of the contour line, where cells on the line have value of 1, and other cells are NA. We set the origin to a value of 2, and tell raster::gridDistance to "find the distance between every cell on the raster and the origin, making sure to follow the cells whose value is not NA (in our case value = 1)."
# find the cell number of the intersection point
cellFromXY(v, point_1 %>% st_as_sf %>% st_coordinates) %>%
{. ->> point_1_cell_number}
# cell number 3075
# set this cell to value of 2
intersecting_contour_rast_3.1[point_1_cell_number] <- 2
intersecting_contour_rast_3.1 %>% plot
# then, use gridDistance to find distances to the origin, from each cell
intersecting_contour_rast_3.1 %>%
raster::raster() %>%
{. ->> int_cont_raster} %>%
raster::gridDistance(origin = 2, omit = NA) %>%
# gridDistance returns values for every cell on the raster,
# so we use mask() to keep only the cells on our original path_1 raster
mask(., int_cont_raster) %>%
{. ->> int_cont_distances} %>%
plot

And to extract the value, we simply use the cell number as an index on the int_cont_distances raster
# now, we find the value of (distance to) the cell number of site 2
# we need the cell numbers of the site(s) first
# first, we have to identify the cell numbers from the sample sites
sites_sf %>%
st_coordinates %>%
cellFromXY(v, .) %>%
{. ->> site_cells}
# 4232 & 958
int_cont_distances[site_cells[2]]
# ~ 425 m
Done!
3.2 - Calculate distance between sites via contour line and intersecting gradient line
To find the distance between the sites, we use the same raster::gridDistance method, but we have to combine the contour and gradient lines (raster versions), and set the origin at either one of the sample sites.
# duplicate the contour line and gradient line
intersecting_contour_rast_3.2 <- intersecting_contour_rast
intersecting_contour_vect_3.2 <- intersecting_contour_vect
# now we make max_gradient_line into a rast
max_gradient_line %>%
rasterize(., v) %>%
{. ->> max_grad_rast}
# ok, now combine the two raster lines
merge(intersecting_contour_rast_3.2, max_grad_rast) %>%
{. ->> path_1}
path_1 %>%
plot
Now, we find the cell numbers of the sample sites, set the value of site 1 (at the end of the gradient line) to 2.
# first, we have to identify the cell numbers from the sample sites
sites_sf %>%
st_coordinates %>%
cellFromXY(v, .) %>%
{. ->> site_cells}
# 4232 & 958
# now, we set one of these cells to a value of 2 in the raster path
path_1[site_cells[1]] <- 2
plot(path_1)
And as above, calculate distance from the origin (now at site 1) to every cell in the raster using raster::gridDistance, and pull out the value for the cell number of site 2 (on the contour line)
# now, calculate the distance from every cell on the raster, to the one with value of 2 (called the origin)
# and, only allow the distance path to follow cells with value of 1
path_1 %>%
raster::raster() %>%
{. ->> path_1_raster} %>%
raster::gridDistance(origin = 2, omit = NA) %>%
# gridDistance returns values for every cell on the raster,
# so we use mask() to keep only the cells on our original path_1 raster
mask(., path_1_raster) %>%
{. ->> path_1_distances} %>%
plot
# now, we find the value of (distance to) the cell number of site 2
path_1_distances[site_cells[2]]
# ~ 615 m
And there you go, it's approx 425 m from site 2 to the gradient line, or 615 m all the way to site 1, via the contour line and the path of maximum gradient.
I know this is probably information overload and the drain_f8.1() function probably warrants a full proper explanation on it's own, but hopefully it can help you with your problem, or for other people in the future.










