Let's consider there is a polygon with near orthogonal edges that is in the range of (70, 89)° or (91, 110)°. We know the sum of angles in a polygon is multiple of 180°.
The question is how to convert a polygon with customized shape to a minimum polygon with right angles.
As a very simple case, let's consider the example below:
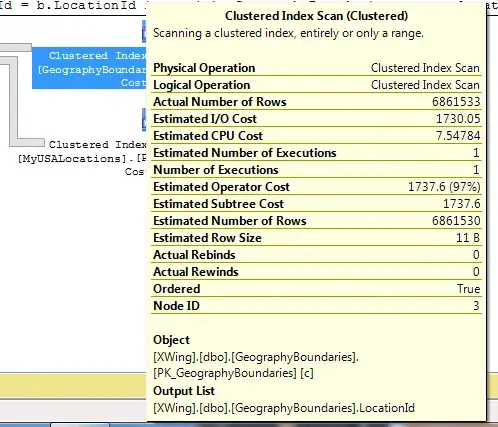
What we want to achieve is, the polygon below:
The number of edges can be more. The example above is just a simple example.