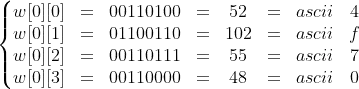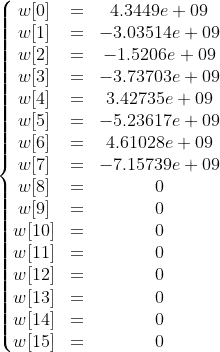Constraining the solutions for linear equations

Question

I'm searching for a way to solve a system of linear equations. Specifically 8 equations with a total of 16 unknown values.

Each unknown value (w[0...15]) is a 32-bit binary value which corresponds to 4 ascii characters written over 8 bits. For example:

For :

I've tried writing this system of linear equations as a single matrix equation. Which gives:

Right now, using the Eigen linear algebra library, I get my 16 solutions (w[0...15]) but all of them are either decimal or null values, which is not what I need. All 16 solutions need to be the equivalent of 4 hexadecimal characters under their binary representation. Meaning integers between 48 and 56 (ascii for '0' to '9'), 65 and 90 (ascii for 'A' to 'Z'), or 97 and 122 (ascii for 'a' to 'z').

Current 16 solutions:

I've found a solution to this problem using something called box-constraints. An example is shown here using python's lsq_linear function which allows the user to specify bounds. It seems Eigen does not let the user specify bounds in its decomposition methods.

Therefore, my question is, how do you get a similar result in C++ using a linear algebra library? Or is there a better way to solve such systems of equations without writing it under a single matrix equation?

Thanks in advance.

Answer 1

Since you're working with linear equations over Z/2³²Z, integer linear programming (as you tagged the question) may be a solution, and algorithms that are inherently floating point are not appropriate. Box constraints are not enough, they won't force the variables to take on integer values. Also, the model shown in the question does not taken into account that multiplying and adding in Z/2³²Z can wrap, which excludes many potential solutions (or perhaps that is intended?) and may make the instance accidentally infeasible when it was intended to be solvable.

ILP can model equations over Z/2³²Z relatively directly (using integer variables between 0 and 2³² and some unconstrained additional variables scaled by 2³² to "absorb" the wraparound), but it tends really struggle with that kind of formulation - I would say it's one of the worst cases for an ILP solver without getting into the "intentionally difficult" cases. A more indirect model with 32x boolean variables is also possible, but this leads to constraints with very large constants and ILP solvers tend to struggle with them too. Overall I do not recommend using ILP for this problem.

What I would recommend for this is an SMT solver that offers the bitvector theory, or as alternatively, a pseudo-boolean solver or plain SAT solver (which would leave the grunt work of implementing boolean circuits and converting them to CNF to you instead of having them builtin in the solver).

Answer 2

If you have more unknowns than equations for sure your system will be indeterminate, the rank of a 8 x 16 matrix is at most 8, thus you have at least 16 degrees of freedom.

Further more if you have bounds to your variables i.e. mixed equalities and inequalities, then your problem is better posed as a linear programming. You can set a dummy objective function c[i] = 0, you could use GLPK but that is a very generic solution. If you want a small code snipped you probably can find a toy implementation of the Simplex method that will satisfy your needs.

Answer 3

I went for an SMT solver as suggested by @harold. Specifically the CVC4 SMT Solver. Here is the code I've written in C++ answering my question about finding the 16 solutions (w[0...15]) for a system of 8 equations, constrained to be ascii characters. I have one last question though. What are pushing and popping for? (slv.push() and slv.pop())

#include <iostream>
#include <cvc4/cvc4.h>

using namespace std;
using namespace CVC4;

int main() {
    // 1. initialize a CVC4 BitVector SMT solver
    ExprManager em;
    SmtEngine slv(&em);
    slv.setOption("incremental", true); // enable incremental solving
    slv.setOption("produce-models", true); // enable models
    slv.setLogic("QF_BV"); // set the bitvector theory logic
    Type bitvector8 = em.mkBitVectorType(size_8); // create a 8-bit wide bit-vector type (4 x 8-bit = 32-bit)

    // 2. create the SMT solver variables
    Expr w[16][4]; // w[0...15] where each w corresponds to 4 ascii characters

    for (int i = 0; i < 16; ++i) {
        for (int j = 0; j < 4; ++j) {
            // a. define w[i] (four ascii characters per w[i])
            w[i][j] = em.mkVar("w" + to_string(i) + to_string(j), bitvector8);

            // b. constraint w[i][0...3] to be an ascii character
            // - digit (0-9) constraint
            // ascii lower bound digit constraint (bit-vector unsigned greater than or equal)
            Expr digit_lower = em.mkExpr(kind::BITVECTOR_UGE, w[i][j], em.mkConst(BitVector(size_8, Integer(48))));

            // ascii upper bound digit constraint (bit-vector unsigned less than or equal)
            Expr digit_upper = em.mkExpr(kind::BITVECTOR_ULE, w[i][j], em.mkConst(BitVector(size_8, Integer(56))));
            Expr digit_constraint = em.mkExpr(kind::AND, digit_lower, digit_upper);

            // - lower alphanumeric character (a-z) constraint
            // ascii lower bound alpha constraint (bit-vector unsigned greater than or equal)
            Expr alpha_lower = em.mkExpr(kind::BITVECTOR_UGE, w[i][j], em.mkConst(BitVector(size_8, Integer(97))));

            // ascii upper bound alpha constraint (bit-vector unsigned less than or equal)
            Expr alpha_upper = em.mkExpr(kind::BITVECTOR_ULE, w[i][j], em.mkConst(BitVector(size_8, Integer(122))));
            Expr alpha_constraint = em.mkExpr(kind::AND, alpha_lower, alpha_upper);

            Expr ascii_constraint = em.mkExpr(kind::OR, digit_constraint, alpha_constraint);
            slv.assertFormula(ascii_constraint);
        }
    }

    // 3. encode the 8 equations
    for (int i = 0; i < 8; ++i) {
        // a. build the multiplication part (index * w[i])
        vector<Expr> left_mult_hand;

        for (int j = 0; j < 16; ++j) {
            vector <Expr> inner_wj;
            for (int k = 0; k < 4; ++k) inner_wj.push_back(w[j][k]);
            Expr wj = em.mkExpr(kind::BITVECTOR_CONCAT, inner_wj);

            Expr index = em.mkConst(BitVector(size_32, Integer(m_unknowns[j])));
            left_mult_hand.push_back(em.mkExpr(kind::BITVECTOR_MULT, index, wj));
        }

        // b. sum each index * w[i]
        slv.push();
        Expr left_hand = em.mkExpr(kind::BITVECTOR_PLUS, left_mult_hand);
        Expr result = em.mkConst(BitVector(size_32, Integer(globalSums.to_ulong())));
        Expr assumption = em.mkExpr(kind::EQUAL, left_hand, result);
        slv.assertFormula(assumption);

        // c. check for satisfiability
        cout << "Result from CVC4 is: " << slv.checkSat(em.mkConst(true)) << endl << endl;
        slv.pop();
    }

    return 0;
}