Premise
I am trying to solve a set of coupled PDEs that describes the diffusion of charged particles with different diffusion coefficients using FiPy. The ultimate goal is to obtain the concentration profile for both species and the electric field.
The geometry is an infinitely long cylinder with radius R. I want to use a non-uniform grid with more points close to the domain walls.
Charged particles diffuse from the center of the domain (left boundary) to the walls of the domain (right boundary). This translates to a Dirichlet boundary condition (B.C.) at the left boundary where both species concentration = 0, and a Neumann B.C. at the right boundary where species flux are 0 to describe radial symmetry. Because the charged species diffuse at different rates, there is an electric field that arises from the space charge. The electric field accelerates the slower species and decelerates the faster species proportional to the field magnitude.
P is the positively charged species concentration and N is negatively charged charged species concentration. E is the space charge electric field.
Issue
I can't seem to get a sensible solution from my code and I think it may be related on how I casted the gradient/divergence terms as a ConvectionTerm:
from fipy import *
import scipy.constants as constant
from fipy.tools import numerix
import numpy as np
## Defining physical constants
pi = constant.pi
m_argon = 6.6335e-26 # kg
k_b = constant.k # J/K
e_0 = constant.epsilon_0 # F/m
q_e = constant.elementary_charge # C
m_e = constant.electron_mass # kg
planck = constant.h
def char_diff_length(L,R):
"""Characteristic diffusion length in a cylinder.
Used for determining the ambipolar diffusion coefficient.
ref: https://doi.org/10.6028/jres.095.035"""
a = (pi/L)**2
b = (2.405/R)**2
c = (a+b)**(1/2)
return c
def L_Debye(ne,Te):
"""Electron Debye screening length given in m.
ne is in #/m3, Te is in K."""
if ne < 3.3e-5:
ne = 3.3e-5
return (((e_0*k_b*Te)/(ne*q_e**2)))**(1/2)
## Setting system parameters
# Operation parameters
Pressure = 1.e5 # ambient pressure Pa
T_g = 400. # background gas temperature K
n_g = Pressure/k_b/T_g # gas number density #/m3
Q_std = 300. # standard volumetric flowrate in sccm
T_e_0 = 11. # plasma temperature ratio T_e/T_g here assumed to be T_e = 0.5 eV and T_g = 500 K
n_e_0 = 1.e20 # electron density in bulk plasma #/m3
# Geometric parameters
R_b = 1.e-3 # radius cylinder m
L = 1.e-1 # length of cylinder m
# Transport parameters
D_ion = 4.16e-6 #m2/s ion diffusion, obtained from https://doi.org/10.1007/s12127-020-00258-z
mu_ion = D_ion*q_e/k_b/T_g # ion electrical mobility using Einstein relation
D_e = 100.68122*D_ion #m2/s electron diffusion
mu_e = D_e*q_e/k_b/T_g # electron electrical mobility using Einstein relation
Lambda = char_diff_length(L,R_b)
debyelength_e = L_Debye(n_e_0,T_g)
gamma = (Lambda/debyelength_e)**2
delta = D_ion/D_e
def d_j(rb,n): #sets the desired spatial steps for mesh
dj = np.zeros(n)
for j in range(n):
dj[j] = 2*rb*(1 - j/n)/n
return dj
#Initializing mesh
dj = d_j(1.,100) # 100 points
mesh = CylindricalGrid1D(dr = dj)
#Declaring cell variables
N = CellVariable(mesh=mesh, value = 1., hasOld = True, name = "electron density")
P = CellVariable(mesh=mesh, value = 1., hasOld = True, name = "ion density")
H = CellVariable(mesh=mesh, value = 0., hasOld = True, name = "electric field")
#Setting boundary conditions
N.constrain(0.,mesh.facesRight) # electron density = 0 at walls
P.constrain(0.,mesh.facesRight)# ion density = 0 at walls
H.constrain(0.,mesh.facesLeft) # electric field = 0 in the center
N.faceGrad.constrain([0.],mesh.facesLeft) # flux of electron = 0 in the center
P.faceGrad.constrain([0.],mesh.facesLeft) # flux of ion = 0 in the center
if __name__ == '__main__':
viewer = Viewer(vars=(P,N))
viewer.plot()
eqn1 = (TransientTerm(var=P) == DiffusionTerm(coeff=delta,var=P)
- ConvectionTerm(coeff=[H.cellVolumeAverage,],var=P)
- ConvectionTerm(coeff=[P.cellVolumeAverage,],var=H))
eqn2 = (TransientTerm(var=N) == DiffusionTerm(var=N)
+ (1/delta)*(ConvectionTerm(coeff=[H.cellVolumeAverage,],var=N)
+ConvectionTerm(coeff=[N.cellVolumeAverage,],var=H)))
eqn3 = (TransientTerm(var=H) == gamma*(ConvectionTerm(coeff=[delta**2,],var=P)
- ConvectionTerm(coeff=[delta,],var=N)
- H*(delta*P.cellVolumeAverage + N.cellVolumeAverage)))
P.setValue(1.)
N.setValue(1.)
H.setValue(0.)
eqn1d = eqn1 & eqn2 & eqn3
timesteps = 1e-5
steps = 100
for i in range(steps):
P.updateOld()
N.updateOld()
H.updateOld()
res = 1e10
sweep = 0
while res > 1e-3 and sweep < 20:
res = eqn1d.sweep(dt=timesteps)
sweep += 1
if __name__ == '__main__':
viewer.plot()
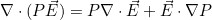, neither of which is a form that FiPy likes. You could write those last two terms as explicit sources, but you shouldn't.
