I am trying to model water pumping with Fipy in a domain where I want to simulate diffusion and advection. Water is extracted from one point, and is discharged in another point. However, I am having issues with regard to the definition of the boundary conditions.
where q is the flow (constant), h is the depth (constant), C is the concentration (transient), and Lx and dx are longitudes (constant).
First, I define the equations (2D Navier-Stokes) to compute the velocity fields. In particular, I impose pressure = zero at the surface, a vertical velocity at the suction/discharge zone (related to the pump nominal flow), and velocity = zero at the bottom.
With regard to the "mass" transport in the domain, I introduce mass fluxes as boundary conditions (however, one problem I have is that I cannot introduce water fluxes, and therefore I cannot take the dillution into account).
I have some questions:
- Can the coefficient (q/Lx) be greater than one when defining the fixed-flux boundary condition? I think that FiPy takes the "mass" from the cells next to the boundary, and thus, if greater than one, it can lead to negative concentrations (which is not possible, in my case).
- Is it possible to move the cells in order to displace water volumes?
- Is it possible to consider the "volume" of the cells to apply the dillution at the top boundary?
This is my code:
coeff_in = (q / Lx_in)
coeff_out = (q / Lx_out)
eqC = (TransientTerm(var = C) == # Transient term
DiffusionTerm(coeff = D, var = C) # Diffusion term
- ConvectionTerm(coeff = Vf, var = C) # Convection term
+ (coeff_out * face_out * (C.faceValue)).divergence # Bottom Boundary Condition (fixed-flux); flow
+ (coeff_in * face_in * Cinput).divergence # Top Boundary Condition (fixed-flux); flow
)
But this produces (obviously!) a concentration of mass at the top, and an extraction at the bottom. Intuitively, if the concentration is the same in all the mesh, the bottom shouldn't have to change (because the volume is extracted and then the mass displaced) and the top should reduce its concentration (because water with lower concentration is introduced and is mixed with the top concentration).

 . In that case, a flux of pure water in at the bottom should be equivalent to a flux of
. In that case, a flux of pure water in at the bottom should be equivalent to a flux of 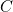 out of the bottom.
out of the bottom.