Fipy Change CellValue between solving timesteps

Question

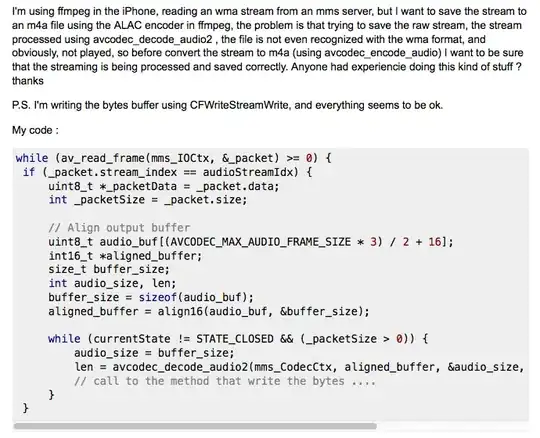
I want to connect a mesh (partial differential equations) with a complex mixture reactor (ordinary differential equations). I want to take the values in one point, solve the ODEs, and reinput the values in the mesh (in which PDEs will be solved).

 # Geometry
Lx = 2   # meters
Ly = 2    # meters
nx = 101 #int((Lx / 0.05) + 1) # nodes
ny = 101 #int((Ly / 0.05) + 1)

# Build the mesh:
mesh = Grid2D(Lx = Lx, Ly = Ly, nx = nx, ny = ny)
X, Y = mesh.cellCenters
xx, yy = mesh.faceCenters

C0_DO = 10. #mg/L # Dissolved Oxygen initial concentration
C0_OM = 5.
T0 = 28. #mg/L # # Temperature
print(f'DO saturation concentration: {calc_DOsat(T0)} mg/L')

# Dissolved oxygen:
C_DO = CellVariable(name="concentration_DO", 
                 mesh=mesh, 
                 value=C0_DO,
                 #hasOld=True
                 )

# Temperature
T = CellVariable(name="temperature", 
                 mesh=mesh,
                 value=T0,
                 #hasOld=True
                 )

C_OM = CellVariable(name="concentration_OM", 
                 mesh=mesh, 
                 value=C0_OM,
                 #hasOld=True
                 )

# Transport parameters (diffusion constants)

# Dissolved oxygen diffusion constant
D_DO = 2. #m2/s
D_DO = FaceVariable(name='DO_diff', mesh=mesh, value=D_DO) # This is necessary to set a fixed-flux boundary condition
D_DO.constrain(0., mesh.exteriorFaces) # This is necessary to set a fixed-flux boundary condition


D_OM = 2.

# Reaction and source terms

O_R = 1. # Re-aeration temperature correction factor (-)
Y_R = 1. #reaeration_rate() # Re-aeration rate (1/day)
DOsat = (14.652 - 0.41022 * T + 0.007991 * T ** 2 - 0.000077774 * T ** 3) # Oxygen saturation concentration (mg/L)
xi_SOD = 0.1 # Sediment Oxygen Demand (BC) (1/day)

# Oxygen transport-reaction
eqDO = (TransientTerm(var = C_DO) == # Transient term
        DiffusionTerm(coeff = D_DO, var = C_DO) # Diffusion term
        + (mesh.facesTop * (Y_R * (O_R ** (T.faceValue - 20)) * ((14.652 - 0.41022 * T.faceValue + 0.007991 * T.faceValue ** 2 - 0.000077774 * T.faceValue ** 3) - C_DO.faceValue))).divergence #Top Boundary Condition (fixed-flux)
        + (mesh.facesBottom * (xi_SOD * C_DO.faceValue)).divergence # Bottom Boundary Condition (fixed-flux)
        )

eqOM = (TransientTerm(var = C_OM) == # Transient term
        DiffusionTerm(coeff = D_OM, var = C_OM) # Diffusion term
        )

eqTOT = eqDO & eqOM


    def reactor_model(C, t):
      k1 = 0.5
      k2 = 0.1
    
      C1 = C[0]
      C2 = C[1]
    
      dC1dt = -k1 * C1
      dC2dt = -k1 * C1
    
      dCdt = [dC1dt, dC2dt]
      
      return dCdt



  # PDESolver hyperparameters
steps = 10
sweeps = 2
dt = 1e-1
reactor_act = True

t = time.time()
for step in range(steps):
  C_DO.updateOld()
  C_OM.updateOld()
  
  for sweep in range(sweeps):
    eqTOT.sweep(dt=dt)

  if reactor_act:
    # Reactor
    r_in = [C_DO([(Lx/2), (0)]).mean(), # Dissolved Oxygen reactor input
            C_OM([(Lx/2), (0)]).mean()  # Organic Matter reactor input
            ]

    print('Reactor input:', r_in)

    # solve ODE
    C = odeint(reactor_model, r_in, np.linspace(0, dt, 10))
    r_out = C[-1]

    print('Reactor output:', r_out)

    # Reinput ODE
    C_DO.setValue(r_out[0], where=(Y >= Ly - mesh.dy / 2 ) & (X <= (Lx/2 + mesh.dx / 2)) & (X > (Lx/2 - mesh.dx / 2)))
    C_OM.setValue(r_out[1], where=(Y >= Ly - mesh.dy / 2 ) & (X <= (Lx/2 + mesh.dx / 2)) & (X > (Lx/2 - mesh.dx / 2)))
  
    C_DO.setValue(r_out[0], where=(Y <= mesh.dy / 2 ) & (X <= (Lx/2 + mesh.dx / 2)) & (X > (Lx/2 - mesh.dx / 2)))
    C_OM.setValue(r_out[1], where=(Y <= mesh.dy / 2 ) & (X <= (Lx/2 + mesh.dx / 2)) & (X > (Lx/2 - mesh.dx / 2)))

elapsed = time.time() - t
print('Calculation completed')
print(f'Runtime: {elapsed/60} minutes')

However, I see that the variables after .setValue are not used for the new iterations. I understand that there is some variation due to the diffusion, but I think this much is not correct:

Reactor input: [9.63329852994412, 4.999999999999067]
Reactor output: [9.1634771  4.53017857]
Reactor input: [9.387521550064774, 4.999830239918787]
Reactor output: [8.9296868  4.54199549]
Reactor input: [9.151030178165843, 4.999737004369599]
Reactor output: [8.70472925 4.55343608]
Reactor input: [8.92773098935664, 4.999650988910076]
Reactor output: [8.49232049 4.56424049]
Reactor input: [8.72052727373096, 4.999567509355334]
Reactor output: [8.29522222 4.57426245]
Reactor input: [8.529743672332394, 4.999485929361331]
Reactor output: [8.11374324 4.5834855 ]
Reactor input: [8.354632596585608, 4.9994060376006795]
Reactor output: [7.94717243 4.59194587]
Reactor input: [8.194109569439474, 4.999327684297063]
Reactor output: [7.79447821 4.59969632]
Reactor input: [8.04703351109057, 4.99925073845838]
Reactor output: [7.65457513 4.60679236]
Reactor input: [7.912305097814226, 4.999175081285443]
Reactor output: [7.5264175  4.61328748]
Calculation completed
Runtime: 0.09242624044418335 minutes

Is there any way to change the CellValues between iterations?

Thank you.