0

I have tried to do a simulation using C++ of the equation of non-local elastica defined by the following system enter image description here

Using the following discretization

enter image description here

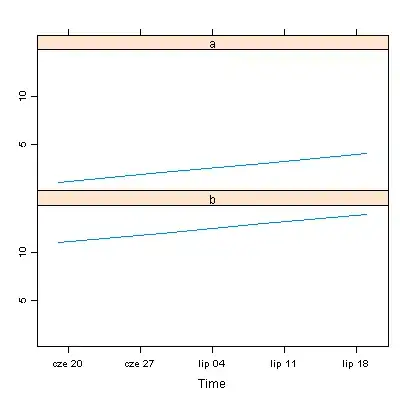
with the boundary condition enter image description here and by sitting lc=1/(6*sqrt(3)), but I did not arrive to the bifurcation diagram like in the following image, enter image description here

This is the code that I have used.

    #include <iostream>
#include <math.h>
#include <fstream>
#include <cstdio>
#define PI 3.14
using namespace std;
main (){
 int i,n,m;
double a=0,b=PI,h,l,BETA=PI*PI;
 double X[500],V[500], T[500];
 cout<<"donne n=";
 cin>>n;
 l=1./(2*n*sqrt(3));
ofstream SOL("eringen.txt");
V[0]=0;
V[100]=0;
X[0]=5;
//SOL << X[0]<<"\t"<< V[0] << endl;

 for (m=1; m<=100; m++)
{
for (i=1; i<=10; i++)
 {
    X[i]=X[i-1]+(1./m)*V[i-1];
        V[i]=V[i-1]-(1./m)*BETA*(1+l*l*V[i-1]*V[i-1])*sin(X[i])*(1./(1-BETA*l*l*cos(X[i])));
        SOL << X[i-1]<<"\t"<< V[i-1] << endl;   
}
}
 FILE *fp = popen("gnuplot", "w");
fprintf(fp,"plot 'eringen.txt'  ;\  pause mouse \n");
cin.get();
 pclose(fp);
}
Hariz Khaled
  • 59
  • 4
  • Why are you varying `m`? From both the formulas and the plot, it looks like `m` is a constant for each curve, and in the plots it's either 1000 or 10000. In your code you are varying `m` from 1 to 100 in a single curve. – G. Sliepen Mar 15 '21 at 08:15
  • @G.Sliepen You're right, also `theta` varied from `0` to `pi` and `beta` from `0` to `8*pi^2`, but I do not understand how to make this implementation. – Hariz Khaled Mar 16 '21 at 10:13
  • Using `for`-loops, but if you only want to get curves for `m = 1000` and `m = 10000`, then write: `for(int m: {1000, 10000}) {...}`. – G. Sliepen Mar 16 '21 at 20:27

0 Answers0