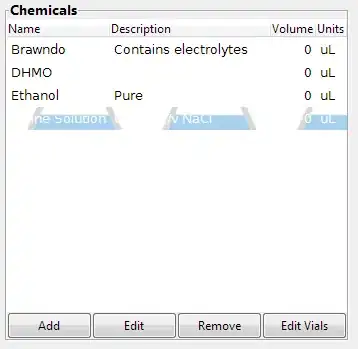
Right now, I'm currently implementing a (potentially non-uniform) B-Spline Curve. One feature that I would like to have is the ability to know where on the curve a control point has the most influence. From my understanding, this is equivalent to solving the maximal point, u, of it's associated B-Spline basis function: N(i, p, u). (where i is the index of the control point, p is the degree, u is the parametric parameter of the curve).
Given a non-decreasing knot vector U, let the i-th B-Spline basis function (of degree p) be defined as follows (from: https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/B-spline/bspline-basis.html):
and a B-spline curve as (from: https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/B-spline/bspline-curve.html):

From my understanding, the possible maximal points for a b-spline basis function are at the endpoints of its domain, as well as when its derivative is zero.
The derivative is as follows (https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/B-spline/bspline-derv.html):
For this question, let's only handle cubic b-spline curves (degree p = 3). And let's notate u_in as u_(i+n) (e.g. u_i0 -> u_i .... u_i3 -> u_(i+3).
The domain of N(i, 3, u) is [u_i0, u_i4).
From my understanding, the derivative N'(i, 3, u) is defined piecewise based on each of it's knot spans: [u_i0, u_i1), [u_i1, u_i2), [u_i2, u_i3), [u_i3, u_i4).
Here are my derivative calculations for each of the knot spans (assuming that u_j < u_(j+1), otherwise that knot span is ignored) :
[u_i0, u_i1]:
For this knot span, the derivative equals zero at u = u_i0.
[u_i3, u_i4]:
For this knot span, the derivative equals zero at u = u_i4.
[u_i1, u_i2]:
This knot span is a more complicated, so I'll solve for N(i, 2, u) and N(i + 1, 2, u) separately.
I plugged these two terms back into the original equation, and then had wolframalpha solve for u in terms of u_i0, u_i1, u_i2, u_i3, u_i4. What got returned to me is this beast:
where t = u...u_j = u_ij.
[u_i2, u_i3]:
Once again, solving for N(i, 2, u) and N(i + 1, 2, u) separately.
I plugged these two terms back into the original equation, and then had wolframalpha solve for u in terms of u_i0, u_i1, u_i2, u_i3, u_i4. What got returned to me is this beast:
where t = u...u_j = u_ij.
..........
So, in totality, my current algorithm is to get the possible maximal points for u. These include all knot span endpoints { u_i0, u_i1, u_i2, u_i3, u_i4 }. They also include the values of u for which the derivate equals zero (taken from the equations above).
After getting all these points, I actually calculate the value of the basis function and return the u which gives me the highest basic function value.
The derivative equations between knot spans [u_i1, u_i2] are quite complex, and I'm not sure how to extend this to a higher degree. Does anyone know of a more extensible, elegant solution?
Thanks!