0

I'm just starting to use R so it is possible that I'm not understanding the functions correctly.

I have length and age data from the literature and I have measured some specimens. I need to find the age of these specimens I measured based on the growth equation that I have calculated from the literature.

Here is a small example from my data:

#Example data
length <- c(0.06,0.087,0.147,0.241,0.615,1.49,2.42)
age <- c(1.3,   2.6,    3.3,    3.9,    5.45,   8,  10.5)

#Polynomial function second degree
growth <- lm(length ~ poly(age, 2, raw=TRUE)-1)

Plot of growth function:
enter image description here

#Need to use this equation to predict x (age) given y (length)
#New y data
mydata_length <- c(0.72,1.82,0.41,0.28)

To calculate age (x) given my data (y) I've tried multiple solutions, and I think the function spline() would be the right solution. Though, it looks like it keeps giving me only 1 of the 2 possible solutions for the polynomial equation, and it is the wrong one. Since it's a growth curve, it starts from the origin and I need the positive solutions to the equation. If I input the coefficients in another software to solve the equation, I can actually get both solutions including the one I need, that I report here. This is a very time consuming solution though, and not great for reproducibility.

#Spline doesn't give the correct results
xvals <- spline(x = growth$fitted.values, xout = mydata_length)$y

#xvals
#[1] -0.01614070  0.09184022 -0.05031075 -0.06537486

#Expected results
#5.88   9.08    4.56    3.85

Plot of growth function with expected results:
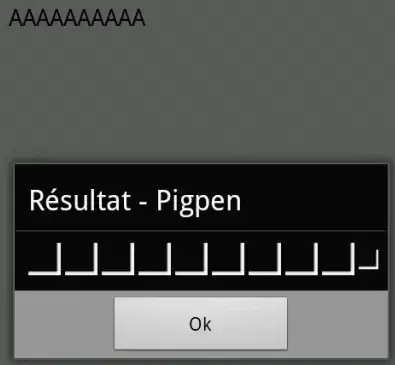
enter image description here

Is there a function within R to find the results I am looking for? I have other data that better fit to a linear regression, so a function to the same but with a linear model would be great to have too.

SOLUTION

I've found a way to obtain what I am looking for, probably not in the prettiest way but it works.

#Calculate age (x) based on my length data (y)

library(polynom)

#Save coefficients
coeffs <- growth$coefficients

#Create function for groth, 0 as intercept
growth_f <- polynomial(c(0, coeffs))

#List of specimen names - row names of y data frame
specimens <- c("sp1", "sp2", "sp3", "sp4")

#Row names for x (calculated age) data frame
rows <- c("discard","keep")

#New data frame with y (length) data
mydata_length_df <- data.frame(mydata_length, row.names = specimens)

#Matrix for calculated age results
x <- matrix(nrow = 2, ncol = nrow(mydata_length_df))
#Make data frame
x <- data.frame(x)
#Set row and column names
rownames(x) <- rows
colnames(x) <- specimens

#Loop to calculate both results of the polynomial for all specimens - second row is the one to keep
for(i in 1:4) {
  x[i] <- data.frame(solve(growth_f, mydata_length_df[i,]))
}        

x
#              sp1       sp2       sp3       sp4
#discard -4.996448 -8.189725 -3.671227 -2.965612
#keep     5.889859  9.083136  4.564638  3.859024

#Transpose to match rest of the data
x <- t(x)

#Data frame with both length and calculated age
new_results <- data.frame(length = mydata_length, calc_age = x[,2])

new_results
#      length  calc_age
#sp1   0.72    5.889859
#sp2   1.82    9.083136
#sp3   0.41    4.564638
#sp4   0.28    3.859024

Plot with expected and calculated results

Agnese Lanzetti
  • 1
  • 1

1 Answers1

0

If length predicts age, then the formula should be age ~ f(length). It is in the form predicted ~ predictors.

#Length predicts age
growth <- lm(age ~ poly(length, 2, raw=TRUE))

#Gridpoints
Length=seq(0, 2.5, length=100)
Age=predict(growth, list(length=grid_x))

#New predictors
lengths=c(0.72,1.82,0.41,0.28)
preds=predict(growth, list(length=lengths))
preds
       1        2        3        4 
5.642787 9.305444 4.204913 3.548846 

actual=c(5.88, 9.08, 4.56, 3.85)
plot(Age, Length, type="n")
lines(Age, Length, col="red")
points(preds, lengths, pch=23, col="purple")
points(actual, lengths, pch=16, col="blue")

enter image description here

Vons
  • 3,277
  • 2
  • 16
  • 19
  • Unfortunately growth curve graphs are standardized the other way around, with age on the x axis and lenght on the y axis. Biologically the 2 things go together so it's not really true that age predicts length or the other way around. It also shouldn't matter, but as you see from your plot, the regression you get is very different and therefore not comparable with previous literature. I need a way to calculate the values of x given a set of y. – Agnese Lanzetti Mar 02 '21 at 01:48
  • @AgneseLanzetti Do you think it matches the literature now? Obviously Length was on the xaxis before and Age on the yaxis, so the graph was reflected across the x=y line. – Vons Mar 02 '21 at 02:06
  • Thanks for this, although in this way the expected results and ones calculated with the function diverge quite a bit since the function is non-symmetrical. I've found a way to solve my issues, it is not elegant but it works. I answer to my question with code below. – Agnese Lanzetti Mar 02 '21 at 13:54