FiPy Transport-reaction with one term depending on two variables on two different equations

Question

I am trying to solve a transport-reaction problem, but I have different solutions depending on the approach. I think that the problem arises if I am trying to solve the coupled equations.

These are the PDEs:

I assume constant Temperature (T in the equations), as well as a constant velocity field (vx, vy).

As you can see, there is an element in the reaction terms that depends on two variables, and which is present in two different variables (the degradation of CBOD depends on the concentration of oxygen CDO, and the concentration of oxygen depends on the amount of CBOD degraded).

This is my code:

# Geometry
Lx = 2  # meters
Ly = 2  # meters
nx = 41 # nodes
ny = 41 # nodes

# Build the mesh:
mesh = Grid2D(Lx=Lx, Ly = Ly, nx=nx, ny=ny)
X,Y = mesh.cellCenters


# Main variable and initial conditions

#Velocity field (constant):
Vf = CellVariable(name='velocity_field',
                 mesh = mesh,
                 value = [vx, vy])

# Dissolved oxygen concentration:
C_DO = CellVariable(name="concentration_DO", 
                 mesh=mesh, 
                 value=0.,
                 hasOld=True)
C_DO.setValue(9.5, where=(Y >= Ly - 0.5))
C_DO.setValue(9.25, where=(Y < Ly - 0.5) & (Y >= Ly - 1.0))
C_DO.setValue(8.9, where=(Y < Ly - 1.0) & (Y >= Ly - 1.5) )
C_DO.setValue(8.8, where=(Y < Ly - 1.5) & (Y >= Ly - 2.0))

# Biochemical Oxygen Demand by Carbonaceous Organic Matter
C_CBOD = CellVariable(name="concentration_CBOD", 
                 mesh=mesh, 
                 value=10.,
                 hasOld=True)

# Biochemical Oxygen Demand by Nitrogenous Organic Matter
C_NBOD = CellVariable(name="concentration_NBOD", 
                 mesh=mesh, 
                 value=10.,
                 hasOld=True)

# Temperature (constant)
T = CellVariable(name="temperature", 
                 mesh=mesh,
                 value=14.4,
                 hasOld=True)


# Transport parameters
D_DO = FaceVariable(name='DO_diff', mesh=mesh, value=1.)
D_DO.constrain(0., mesh.exteriorFaces)

D_CBOD = 1.
D_NBOD = 1.


## Reaction & source terms

# DO
O_r = 1.025
K_r = 1.

# CBOD:
O_CBOD = 1.047
K_CBOD_0 = 0.2
K_CBOD = K_CBOD_0 / DOsat
CBOD_reaction_coeff = K_CBOD * (O_CBOD ** (T - 20))

# NBOD:
O_NBOD = 1.047
K_NBOD_0 = 0.2
K_NBOD = K_NBOD_0 / DOsat
NBOD_reaction_coeff = K_NBOD * (O_NBOD ** (T - 20))

# Boundary conditions
### fixed flux, atmospheric exchange, included in the main equation.

# Equations definition:

# DO transport-reaction
eqDO = (TransientTerm(var = C_DO) == 
        DiffusionTerm(coeff=D_DO, var = C_DO) 
        - ConvectionTerm(coeff=Vf, var=C_DO)
        + ImplicitSourceTerm(coeff= -1 * CBOD_reaction_coeff * C_CBOD, var=C_DO) 
        + ImplicitSourceTerm(coeff= -1 * NBOD_reaction_coeff * C_NBOD, var=C_DO) 
        + (mesh.facesTop * (K_r * (O_r ** (T.faceValue - 20)) * ((14.652 - 0.41022 * T.faceValue + 0.007991 * T.faceValue ** 2 - 0.000077774 * T.faceValue ** 3) - C_DO.faceValue))).divergence))
    
# CBOD transport-reaction
eqCBOD = (TransientTerm(var = C_CBOD) == 
          DiffusionTerm(coeff=D_CBOD, var = C_CBOD) 
          - ConvectionTerm(coeff=Vf, var=C_CBOD) 
          + ImplicitSourceTerm(coeff= -1 * CBOD_reaction_coeff * C_DO, var=C_CBOD))

# NBOD transport-reaction
eqNBOD = (TransientTerm(var = C_NBOD) == 
          DiffusionTerm(coeff=D_NBOD, var = C_NBOD) 
          - ConvectionTerm(coeff=Vf, var=C_NBOD) 
          + ImplicitSourceTerm(coeff= -1 * NBOD_reaction_coeff * C_DO, var=C_NBOD))

eqQ = eqDO & eqCBOD & eqNBOD

# PDESolver hyperparameters
steps = 230 
dt = 1e-2

for step in range(steps):
  C_DO.updateOld()
  C_CBOD.updateOld()
  C_NBOD.updateOld()

  eqQ.solve(dt=dt)

Depending on whether I solve the three equations separately (eqDO.solve(dt=dt), eqCBOD.solve(dt=dt), eqNBOD.solve(dt=dt)), or coupled in a system (eqQ.solve(dt=dt)), I obtain different results (same distribution in the mesh, but different values). I do not know if I can have this term with different variables in two different equations; for instance:

eqDO = ... + ImplicitSourceTerm(coeff= -1 * CBOD_reaction_coeff * C_CBOD, var=C_DO) <--- Is this OK?
eqCBOD = ... + ImplicitSourceTerm(coeff= -1 * CBOD_reaction_coeff * C_DO, var=C_CBOD) <--- Is this OK?

I would like to solve the concentrations CBOD, NBOD and DO together. Can I define the previous elements this way when solving the equations together? Or is it better to solve the equations one by one if I have those terms?

Answer 1

• The conservation properties are probably better if reaction terms are exactly the same between their respective governing equations, but if you sweep (which you should), it probably doesn't matter.
• You need to sweep. You have non-linear dependencies between the equations. It doesn't matter whether you solve as a coupled system or if you solve the equations successively. Anything that appears as the coefficient of a Term, which can change as a result of the solution, must be swept.
• When every var=? in every Term in an equation specifies the same variable, there is no coupling between your equations, so there is no point in using the & notation. You just use more memory to probably do a worse job of solving three independent equations.
• Even if you adjust some of your var=? assignments to introduce coupling, you'll generally get solutions more readily by not coupling at first. Coupling can help convergence, but it often wreaks havoc on stability.
• Similarly, judicious use of ImplicitSourceTerm can help convergence, but often just confuses things when you're trying to get a set of equations to solve at all. I would write these sources explicitly, e.g., - CBOD_reaction_coeff * C_CBOD * C_DO until you know everything is working.
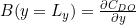• describes a constraint on gradient, but 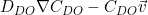(mesh.facesTop * blahblah).divergence imposes a boundary flux. For your equation, the flux is . You should use C_DO.faceGrad.constrain(...).