Simulate CDF curve for penetration/adoption extrapolation

Question

I'd like to be able to plot a line like the cumulative distribution function for the normal distribution, because it's useful for simulating the adoption curve:

Specifically, I'd like to be able to use initial data (percentage adoption of a product) to extrapolate what the rest of that curve would look like, to give a rough estimate of the timeline to each of the phases. So, for example, if we got to 10% penetration by 30 days and 20% penetration by 40 days, and we try to fit this curve, I'd like to know when we're going to get to 80% penetration (vs another population that may have taken 50 days to get to 10% penetration).

So, my question is, how could I go about doing this? I would ideally be able to provide initial data (time and penetration), and use python (e.g. matplotlib) to plot out the rest of the chart for me. But I don't know where to start! Can anyone point me in the right direction?

(Incidentally, I also posted this question on CrossValidated, but I wasn't sure whether it belonged there, as it's a stats question, or here, as it's a python question. Apologies for duplication!)

Answer 1

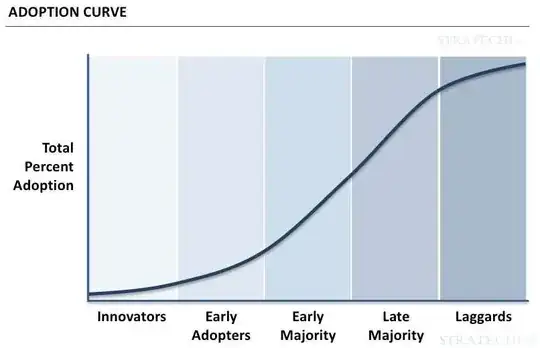
The cdf can be calculated via scipy.stats.norm.cdf(). Its ppf can be used to help map the desired correspondences. scipy.interpolate.pchip can then create a function to so that the transformation interpolates smoothly.

import matplotlib.pyplot as plt
from matplotlib.ticker import PercentFormatter
import numpy as np
from scipy.interpolate import pchip  # monotonic cubic interpolation
from scipy.stats import norm

desired_xy = np.array([(30, 10), (40, 20)])  # (number of days, percentage adoption)
# desired_xy = np.array([(0, 1), (30, 10), (40, 20), (90, 99)])
labels = ['Innovators', 'Early\nAdopters', 'Early\nMajority', 'Late\nMajority', 'Laggards']
xmin, xmax = 0, 90  # minimum and maximum day on the x-axis

px = desired_xy[:, 0]
py = desired_xy[:, 1] / 100

# smooth function that transforms the x-values to the  corresponding spots to get the desired y-values
interpfunc = pchip(px, norm.ppf(py))

fig, ax = plt.subplots(figsize=(12, 4))
# ax.scatter(px, py, color='crimson', s=50, zorder=3)  # show desired correspondances
x = np.linspace(xmin, xmax, 1000)
ax.plot(x, norm.cdf(interpfunc(x)), lw=4, color='navy', clip_on=False)

label_divs = np.linspace(xmin, xmax, len(labels) + 1)
label_pos = (label_divs[:-1] + label_divs[1:]) / 2
ax.set_xticks(label_pos)
ax.set_xticklabels(labels, size=18, color='navy')
min_alpha, max_alpha = 0.1, 0.4
for p0, p1, alpha in zip(label_divs[:-1], label_divs[1:], np.linspace(min_alpha, max_alpha, len(labels))):
    ax.axvspan(p0, p1, color='navy', alpha=alpha, zorder=-1)
    ax.axvline(p0, color='white', lw=1, zorder=0)
ax.axhline(0, color='navy', lw=2, clip_on=False)
ax.axvline(0, color='navy', lw=2, clip_on=False)
ax.yaxis.set_major_formatter(PercentFormatter(1))
ax.set_xlim(xmin, xmax)
ax.set_ylim(0, 1)
ax.set_ylabel('Total Adoption', size=18, color='navy')
ax.set_title('Adoption Curve', size=24, color='navy')
for s in ax.spines:
    ax.spines[s].set_visible(False)
ax.tick_params(axis='x', length=0)
ax.tick_params(axis='y', labelcolor='navy')
plt.tight_layout()
plt.show()

Using just two points for desired_xy the curve will be linearly stretched. If more points are given, a smooth transformation will be applied. Here is how it looks like with [(0, 1), (30, 10), (40, 20), (90, 99)]. Note that 0 % and 100 % will cause problems, as they lie at minus at plus infinity.