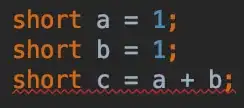
I have a matrix A with shape=(N, N) and a matrix B with the same shape=(N, N). I am constructing a matrix M using the following einsum (using the opt_einsum library):
M = oe.contract('nm,in,jm,pn,qm->ijpq', A, B, B, B, B)
This is evaluating the following sum:
This yeilds matrix M with shape (N, N, N, N). I then reshape this to a 2D array of shape (N**2, N**2)
M = M.reshape((N**2, N**2))
This must be 2D as it is treated as a linear operator.
I want to use the sparse library, as M is sparse, and becomes too large to store for large N. I can make A and B sparse, and insert them into the oe.contract.
The problem is, sparse only supports 2D arrays and so fails to produce the 4D output of shape (N, N, N. N). Is there a way to combine the einsum and reshape steps to allow sparse to be used in this way, as the final shape of M is 2D?