I am trying to visualize the trajectory of multiple participants in a virtual room using R. I have a participant entering from the right (black square) and moving toward the left, where there is an exit door (red square). Sometimes there is an obstacle right in the middle of the room (circle), and the participant goes around it. To visualize multiple participants’ trajectories on the same graph (i.e., multiple lines), I have used the function plot to set up the plot itself (and the first line) and then I have used the function lines to add other trajectories after that. Below you can see an example with two lines; in the experiment, I have many more (as now I have collected data from about 20 participants.)
library(shape)
# black line
pos_x <- c(5.04,4.68,4.39,4.09,3.73,3.37,3.07,2.77,2.47,2.11)
pos_z <- c(0.74,0.69,0.64,0.60,0.56,0.52,0.50,0.50,0.50,0.51)
df1 <- cbind.data.frame(pos_x,pos_z)
x.2 <- df1$pos_x
z.2 <- df1$pos_z
plot(x.2,z.2,type="l", xlim=range(x.2), ylim=c(-1,3.5), xlab="x", ylab="z", main = "Two trajectories")
filledrectangle(wx = 0.2, wy = 0.2,col = "black", mid = c(5.16, 1), angle = 0)
filledrectangle(wx = 0.2, wy = 0.2,col = "red", mid = c(2, 1), angle = 0)
plotcircle(mid = c(3.4, 1), r = 0.05)
# red line
pos_x <- c(5.14,4.84,4.24,3.64,3.34,2.74,2.15)
pos_z <- c(0.17,0.13,0.01,-0.2,0.01,0.10,0.17)
df2 <- cbind.data.frame(pos_x,pos_z)
x.3 <- df2$pos_x
z.3 <- df2$pos_z
lines(x.3, z.3, xlim=range(x.3), ylim=c(-1,3.5), pch=16, col="red")
What I would like to do now is to find the average between these two lines. Ideally, I would like to be able to average multiple lines and add an interval for the standard deviation.
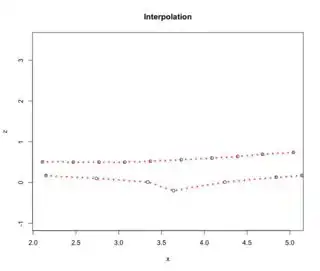
The first thing I have tried is to build an interpolation; the problem is that the start and end point are different, so I cannot average the points:
plot(x.2, z.2, xlim=range(x.2), ylim=c(-1,3.5), xlab="x", ylab="z", main = "Interpolation")
points(approx(x.2, z.2), col = 2, pch = "*")
points(x.3, z.3)
points(approx(x.3, z.3), col = 2, pch = "*")
I have then found a suggestion here: use the R library dtw.
I have looked up the library and the companion paper.
This is a typical example from the paper, in which "two non-overlapping windows" are extracted from a reference electrocardiogram. The dataset "aami3a" is a time series object.
library("dtw")
data("aami3a")
ref <- window(aami3a, start = 0, end = 2)
test <- window(aami3a, start = 2.7, end = 5)
alignment <- dtw(test, ref)
alignment$distance
The problem is that in all these examples the data is either structured as a time series object or the two lines are functions of a common matrix (see also the R quickstart example in the documentation and this other tutorial.)
How can I reorganize my data to make the function work? Or do you know of any other way to create an average?