Here is a breakdown of your code, with some suggestions for improvement, and extra explanations. Working through it carefully will show you what is going on. The results you are getting are completely expected. I will propose a common solution at the end.
First set up your units correctly. I assume that you are dealing with seconds, not microseconds. You can adjust later as long as you stay consistent.
Establish the period and frequency of the sampling. This means that the Nyquist frequency for the FFT will be 500Hz:
T = 0.001 # 1ms sampling period
fs = 1 / T # 1kHz sampling frequency
Make a time domain of 30e3 points. The half domain will contain 15000 points. That implies a frequency resolution of 500Hz / 15k = 0.03333Hz.
x = np.arange(0, 30, T) # time domain
n = x.size # number of points: 30000
Before doing anything else, we can define our time domain right here. I prefer a more intuitive approach than what you are using. That way you don't have to redefine T or introduce the auxiliary variable k. But as long as the results are the same, it does not really matter:
F = np.linspace(0, 1 - 1/n, n) / T # Notice F[1] = 0.03333, as predicted
Now define the signal. You picked ff = 0.2. Notice that 0.2Hz. 0.2 / 0.03333 = 6, so you would expect to see your peak in exactly bin index 6 (F[6] == 0.2). To better illustrate what is going on, let's take ff = 0.22. This will bleed the spectrum into neighboring bins.
ff = 0.22
y = np.sin(2 * np.pi * ff * x)
Now take the FFT:
Y = np.fft.fft(y) / n
maxbin = np.abs(Y).argmax() # 7
maxF = F[maxbin] # 0.23333333: This is the nearest bin
Since your frequency bins are 0.03Hz wide, the best resolution you can expect 0.015Hz. For your real data, which has much lower resolution, the error is much larger.
Now let's take a look at what happens when you halve the data size. Among other things, the frequency resolution becomes smaller. Now you have a maximum frequency of 500Hz spread over 7.5k samples, not 15k: the resolution drops to 0.066666Hz per bin:
n2 = n // 2 # 15000
F2 = np.linspace(0, 1 - 1 / n2, n2) / T # F[1] = 0.06666
Y2 = np.fft.fft(y[:n2]) / n2
Take a look what happens to the frequency estimate:
maxbin2 = np.abs(Y2).argmax() # 3
maxF2 = F2[maxbin2] # 0.2: This is the nearest bin
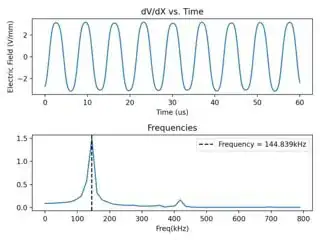
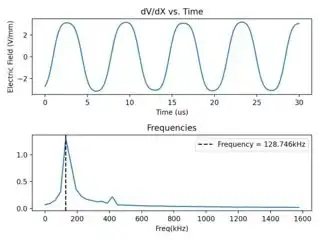
Hopefully, you can see how this applies to your original data. In the full FFT, you have a resolution of ~16.1 per bin with the full data, and ~32.2kHz with the half data. So your original result is within ~±8kHz of the right peak, while the second one is within ~±16kHz. The true frequency is therefore between 136kHz and 144kHz. Another way to look at it is to compare the bins that you showed me:
full: 128.7 144.8 160.9
half: 96.6 128.7 160.9
When you take out exactly half of the data, you drop every other frequency bin. If your peak was originally closest to 144.8kHz, and you drop that bin, it will end up in either 128.7 or 160.9.
Note: Based on the bin numbers you show, I suspect that your computation of frq is a little off. Notice the 1 - 1/n in my linspace expression. You need that to get the right frequency axis: the last bin is (1 - 1/n) / T, not 1 / T, no matter how you compute it.
So how to get around this problem? The simplest solution is to do a parabolic fit on the three points around your peak. That is usually a sufficiently good estimator of the true frequency in the data when you are looking for essentially perfect sinusoids.
def peakF(F, Y):
index = np.abs(Y).argmax()
# Compute offset on normalized domain [-1, 0, 1], not F[index-1:index+2]
y = np.abs(Y[index - 1:index + 2])
# This is the offset from zero, which is the scaled offset from F[index]
vertex = (y[0] - y[2]) / (0.5 * (y[0] + y[2]) - y[1])
# F[1] is the bin resolution
return F[index] + vertex * F[1]
In case you are wondering how I got the formula for the parabola: I solved the system with x = [-1, 0, 1] and y = Y[index - 1:index + 2]. The matrix equation is
[(-1)^2 -1 1] [a] Y[index - 1]
[ 0^2 0 1] @ [b] = Y[index]
[ 1^2 1 1] [c] Y[index + 1]
Computing the offset using a normalized domain and scaling afterwards is almost always more numerically stable than using whatever huge numbers you have in F[index - 1:index + 2].
You can plug the results in the example into this function to see if it works:
>>> peakF(F, Y)
0.2261613409657391
>>> peakF(F2, Y2)
0.20401580936430794
As you can see, the parabolic fit gives an improvement, however slight. There is no replacement for just increasing frequency resolution through more samples though!