You can solve the problem by finding a matrix that transforms points from positions (0, 0), (0, 1), ... (2, 2) onto the given points.
Although the grid has only 5 degrees of freedom (position of the origin + angle + scale), it is easier to define the transformation using 2x3 matrix A, because the problem can be made linear in this case.
Let a point with index (x0, y0) to be transformed into point (x0', y0') on the grid, for example (0, 0) -> (2, 5.464) and let a_ij be coefficients of matrix A. Then this pair of points results in 2 equations:
a_00 * x0 + a_01 * y0 + a_02 = x0'
a_10 * x0 + a_11 * y0 + a_12 = y0'
The unknowns are a_ij, so these equations can be written in form
a_00 * x0 + a_01 * y0 + a_02 + a_10 * 0 + a_11 * 0 + a_12 * 0 = x0'
a_00 * 0 + a_01 * 0 + a_02 * 0 + a_10 * x0 + a_11 * y0 + a_12 = y0'
or in matrix form
K0 * (a_00, a_01, a_02, a_10, a_11, a_12)^T = (x0', y0')^T
where
K0 = (
x0, y0, 1, 0, 0, 0
0, 0, 0, x0, y0, 1
)
These equations for each pair of points can be combined in a single equation
K * (a_00, a_01, a_02, a_10, a_11, a_12)^T = (x0', y0', x1', y1', ..., xn', yn')^T
or K * a = b
where
K = (
x0, y0, 1, 0, 0, 0
0, 0, 0, x0, y0, 1
x1, y1, 1, 0, 0, 0
0, 0, 0, x1, y1, 1
...
xn, yn, 1, 0, 0, 0
0, 0, 0, xn, yn, 1
)
and (xi, yi), (xi', yi') are pairs of corresponding points
This can be solved as a non-homogeneous system of linear equations. In this case the solution will minimize sum of squares of distances from each point to nearest grid intersection. This transform can be also considered to maximize overall likelihood given the assumption that points are shifted from grid intersections with normally distributed noise.
a = (K^T * K)^-1 * K^T * b
This algorithm can be easily implemented if there is a linear algebra library is available. Below is an example in Python:
import numpy as np
n_points = 9
aligned_points = [(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)]
grid_points = [(2, 5.464), (3.732, 6.464), (5.464, 7.464), (3, 3.732), (4.732, 4.732), (6.464, 5.732), (4, 2), (5.732, 3), (7.464, 4)]
K = np.zeros((n_points * 2, 6))
b = np.zeros(n_points * 2)
for i in range(n_points):
K[i * 2, 0] = aligned_points[i, 0]
K[i * 2, 1] = aligned_points[i, 1]
K[i * 2, 2] = 1
K[i * 2 + 1, 3] = aligned_points[i, 0]
K[i * 2 + 1, 4] = aligned_points[i, 1]
K[i * 2 + 1, 5] = 1
b[i * 2] = grid_points[i, 0]
b[i * 2 + 1] = grid_points[i, 1]
# operator '@' is matrix multiplication
a = np.linalg.inv(np.transpose(K) @ K) @ np.transpose(K) @ b
A = a.reshape(2, 3)
print(A)
[[ 1. 1.732 2. ]
[-1.732 1. 5.464]]
Then the parameters can be extracted from this matrix:
theta = math.degrees(math.atan2(A[1, 0], A[0, 0]))
scale_x = math.sqrt(A[1, 0] ** 2 + A[0, 0] ** 2)
scale_y = math.sqrt(A[1, 1] ** 2 + A[0, 1] ** 2)
origin_x = A[0, 2]
origin_y = A[1, 2]
theta = -59.99927221917264
scale_x = 1.99995599951599
scale_y = 1.9999559995159895
origin_x = 1.9999999999999993
origin_y = 5.464
However there remains a minor issue: matrix A corresponds to an affine transform. This means that grid axes are not guaranteed to be perpendicular. If this is a problem, then the first two columns of the matrix can be modified in a such way that the transform preserves angles.
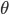between one side and x axis, and increments 
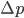and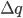 
- please see the figure below.
