Why is softmax classifier gradient divided by batch size (CS231n)?

Question

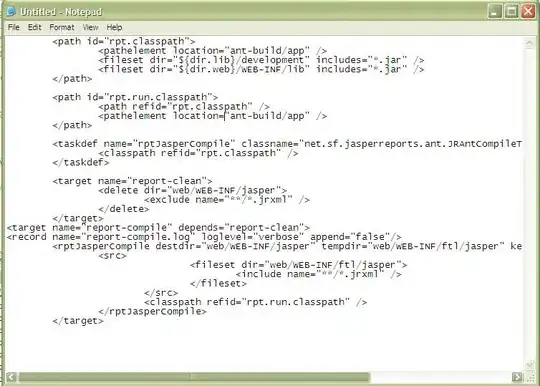
Question

In CS231 Computing the Analytic Gradient with Backpropagation which is first implementing a Softmax Classifier, the gradient from (softmax + log loss) is divided by the batch size (number of data being used in a cycle of forward cost calculation and backward propagation in the training).

Please help me understand why it needs to be divided by the batch size.

The chain rule to get the gradient should be below. Where should I incorporate the division?

• Derivative of Softmax loss function

Code

N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels

#Train a Linear Classifier

# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in range(200):

  # evaluate class scores, [N x K]
  scores = np.dot(X, W) + b

  # compute the class probabilities
  exp_scores = np.exp(scores)
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]

  # compute the loss: average cross-entropy loss and regularization
  correct_logprobs = -np.log(probs[range(num_examples),y])
  data_loss = np.sum(correct_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W)
  loss = data_loss + reg_loss
  if i % 10 == 0:
    print "iteration %d: loss %f" % (i, loss)

  # compute the gradient on scores
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples                      # <---------------------- Why?

  # backpropate the gradient to the parameters (W,b)
  dW = np.dot(X.T, dscores)
  db = np.sum(dscores, axis=0, keepdims=True)

  dW += reg*W # regularization gradient

  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db

Answer 1

It's because you are averaging the gradients instead of taking directly the sum of all the gradients.

You could of course not divide for that size, but this division has a lot of advantages. The main reason is that it's a sort of regularization (to avoid overfitting). With smaller gradients the weights cannot grow out of proportions.

And this normalization allows comparison between different configuration of batch sizes in different experiments (How can I compare two batch performances if they are dependent to the batch size?)

If you divide for that size the gradients sum it could be useful to work with greater learning rates to make the training faster.

This answer in the crossvalidated community is quite useful.

Answer 2

Came to notice that the dot in dW = np.dot(X.T, dscores) for the gradient at W is Σ over the num_sample instances. Since the dscore, which is probability (softmax output), was divided by the num_samples, did not understand that it was normalization for dot and sum part later in the code. Now understood divide by num_sample is required (may still work without normalization if the learning rate is trained though).

I believe the code below explains better.

# compute the gradient on scores
dscores = probs
dscores[range(num_examples),y] -= 1

# backpropate the gradient to the parameters (W,b)
dW = np.dot(X.T, dscores) / num_examples
db = np.sum(dscores, axis=0, keepdims=True) / num_examples