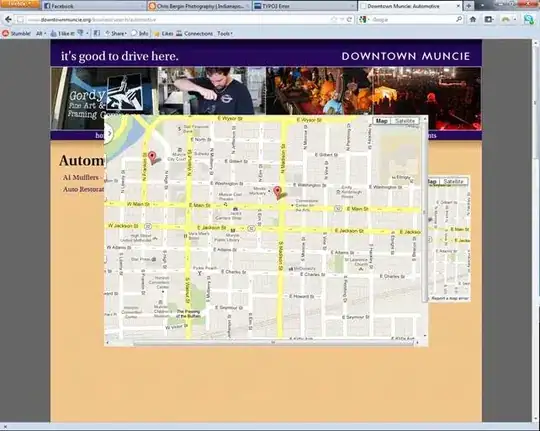
Please take a look at my solution below, and study how it differs from your own.
function [th2,th3,th4] = q65270276()
[th2,th3,th4] = lorenzSystem();
hF = figure(); hAx = axes(hF);
plot(hAx, deg2rad(th2), deg2rad(th3), deg2rad(th2), deg2rad(th4));
xlabel(hAx, '\theta_2')
xticks(hAx, 0:pi/3:2*pi);
xticklabels(hAx, {'$0$','$\frac{\pi}{3}$','$\frac{2\pi}{3}$','$\pi$','$\frac{4\pi}{3}$','$\frac{5\pi}{3}$','$2\pi$'});
hAx.TickLabelInterpreter = 'latex';
yticks(hAx, 0:pi/6:pi);
yticklabels(hAx, {'$0$','$\frac{\pi}{6}$','$\frac{\pi}{3}$','$\frac{\pi}{2}$','$\frac{2\pi}{3}$','$\frac{5\pi}{6}$','$\pi$'});
set(hAx, 'XLim', [0 2*pi], 'YLim', [0 pi], 'FontSize', 16);
grid(hAx, 'on');
legend(hAx, '\theta_3', '\theta_4')
end
function [th2,th3,th4] = lorenzSystem()
th2 = (0:2.5:360).';
[th3,th4] = deal(zeros(size(th2)));
% Define geometry:
r1 = 40;
r2 = 15;
r3 = 50;
r4 = 45;
% Define the residual:
res = @(q,X)[r2*cosd(q)+r3*cosd(X(1))-r4*cosd(X(2))-r1; ... Δx=0
r2*sind(q)+r3*sind(X(1))-r4*sind(X(2))]; % Δy=0
% Define the Jacobian:
J = @(X)[-r3*sind(X(1)), r4*sind(X(2));
r3*cosd(X(1)), -r4*cosd(X(2))];
X0 = [acosd((45^2-25^2-50^2)/(-2*25*50)); 180-acosd((50^2-25^2-45^2)/(-2*25*45))]; % Accurate guess
maxIter = 500;
tolX = 1e-6;
for idx = 1:numel(th2)
X = X0;
Xold = X0;
err = zeros(maxIter, 1); % Preallocation
for it = 1:maxIter
% Update the guess
f = res( th2(idx), Xold );
X = Xold - J(Xold) \ f;
% X = X - pinv(J(X)) * res( q(idx), X ); % May help when J(X) is close to singular
% Determine convergence
err(it) = (X-Xold).' * (X-Xold);
if err(it) < tolX
break
end
% Update history
Xold = X;
end
% Unpack and store θ₃, θ₄
th3(idx) = X(1);
th4(idx) = X(2);
% Update X0 for faster convergence of the next case:
X0 = X;
end
end
Several notes:
All computations are performed in degrees.
The specific plotting code I used is less interesting, what matters is that I defined all θ₂ in advance, then looped over them to find θ₃ and θ₄ (without recursion, as was done in your own implementation).
The initial guess (actually, analytical solution) for the very first case (θ₂=0) can be found by solving the problem manually (i.e. "on paper") using the law of cosines. The solver also works for other guesses, but you might need to increase maxIter. Also, for certain guesses (e.g. X(1)==X(2)), the Jacobian is ill-conditioned, in which case you can use pinv.
If my computation is correct, this is the result: