Mean Squared Displacement
Definition of mean squared displacement
To make sure we are agreeing on the definition, the mean squared displacement (MSD) is the mean of the squared distance from origin of a collection of particles (in our case, walkers) at a specific step.
Since we are in 1D, the distance is simply the absolute position : distance at time t = | path[t] |
To get the MSD at step t, we must take all the squared positions at step t, then take the mean of the resulting array.
That means : MSD at step t == (path[:, t]**2).mean() (the element-wise squaring makes it useless to take the absolute values)
path[:, t] means here : the positions of each walker at step t.
Generating paths
We must edit your code a bit to have several independant paths.
walkers = 50 # Example for 50 walkers
path = []
steps = 60
for walker in range(walkers):
walker_path=[0]
position = 0
for i in range(1, steps):
move = np.random.randint(0, 2)
if move == 0: position += -1
else: position += 1
walker_path.append(position)
path.append(walker_path)
path = np.array(path)
As a sidenote, you could also use random.choice to randomly pick -1 or 1 directly, like so:
for i in range(1, steps):
position += np.random.choice([-1, 1])
walker_path.append(position)
From now, path is a 2D array : a row per walker path.
Getting MSD at each step
To get all the MSD at every steps, we vary t from 1 to the number of steps.
You can do it inside a list comprehension in Python (and getting rid of your calcMSD function):
msd = [(path[:, i]**2).mean() for i in range(1, steps)]
# you could also put range(1, len(path[0]))
Result
Your function was not adapted to plot several walkers.
The proposed solution will give you something like this :
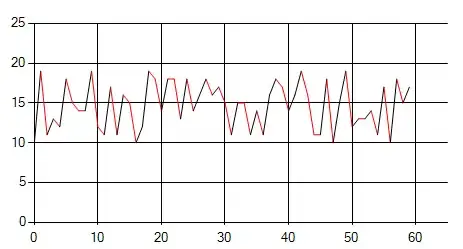
What you want
I hope I understood what you truly wanted. I don't know how it's called but it can also be calculated in a list comprehension. Considering the path for a single walker :
not_msd = [(np.array([path[start:start+sep+1] for start in range(steps-sep)])**2).mean() for sep in range(1, steps)]
We go from start to start + step to get the difference between two positions that are step steps apart. We reproduce this operation, starting from 0 to the end of the list. Then we square the obtained list and take the mean.
We do that for all step size : 1 to the whole length.
Result :