SLR(1) Parser and epsilon involved

Question

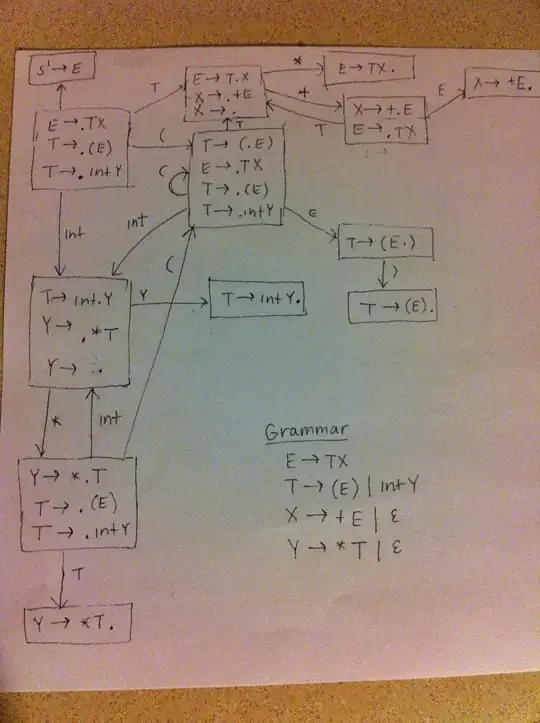
Let's suppose I have the following grammar:

S → X  
X → a | ϵ

If that grammar wouldn't have ϵ involved, I would construct the first state like:

S' → .S
S → .X
X → .a

but what about the ϵ symbol? Should I include:

X → .ϵ

too?

If so... when creating the next states... should I do GOTO(Io,ϵ), being Io that first state?

score 17 · Answer 1 · answered Apr 28 '12 at 07:04

17

I agree with Howard. Your state in the DFA should contain the item: x → . Here's a DFA I drew for an SLR(1) parser that recognizes a grammar that uses two epsilon productions: SLR(1) DFA

answered Apr 28 '12 at 07:04

Rose Perrone

61,572
58
208
243

I have a problem with this scanned example. Let's have a look at T(n): T -> .(E) goto(T(n), () = { [T->(.E)], [E->.TX], [T->.(E)] , [T->.intY]} if so, then consequently, for T(n+1): X->.+E should I not have: goto(T(n+1), +) = {[X->+.E], [E->.TX], [T->.(E)] , [T-> .intY]} ? Instead in the example I have: goto(T(n+1), +) = {[X->+.E], [E->.TX]} Why we are not including in goto(T(n+1), +) productions for T? – Joanna Jun 22 '17 at 11:23
You are correct @joanna. While I do not understand what you mean by T(n) and T(n+1), the LR state you are referring to, namely {[X->+.E], [E->.TX]} should include productions for T via prediction. In the current formulation there is no way to progress from the given state since there are no terminals to the right of the dot. – corwin.amber Aug 14 '17 at 17:36

score 11 · Accepted Answer · answered Jun 28 '11 at 04:44

11

Since ϵ is not a terminal itself you have to remove it from your rule which gives you

X → .

Then later you won't have any strange GOTO with "symbol" ϵ but instead your state

S' → S.

is an accepting state in your graph.

answered Jun 28 '11 at 04:44

Howard

38,639
9
64
83

That makes sense. Do you have any example of a LR parser applied to a grammar where an epsilon is involved :? – Oscar Mederos Jun 28 '11 at 04:55
@Oscar Unfortunately I do not have an example which demonstrates how to proceed. But it should be straightforward to build this by hand based on your grammar. – Howard Jun 28 '11 at 16:23
I confirmed it in a book I read today ;) It is exactly as you said. Thank you for your response. – Oscar Mederos Jun 28 '11 at 18:15
So you mean that epsilon elimination should be applied ? – Parsa Noori Nov 02 '21 at 15:12

SLR(1) Parser and epsilon involved

2 Answers2