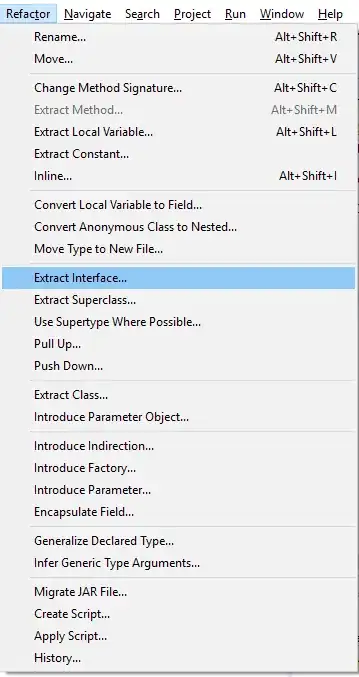
I have a data-set and I'm exploring potential exponential fits to the data using eye-balled estimations and estimations via maximum likelihood methods. I'm finding a huge discrepancy in one of the parameter fits and I'm not sure how to reconcile between what I expect vs the stats. I'm wondering if the dnorm in the ML function is appropriate or perhaps my plotting from the estimates isn't correct?
Data fit to exponential function type a + exp(-x * b) + c
y.size <- c(2.69,4.1,8.04,3.1,5.27,5.033333333,3.2,7.25,6.29,4.55,6.1,2.65,3.145,3.775,3.46,5.73,5.31,4.425,3.725,4.32,5,3.09,5.25,5.65,3.48,6.1,10,9.666666667,6.06,5.9,2.665,4.32,3.816666667,3.69,5.8,5,3.72,3.045,4.485,3.642857143,5.5,6.333333333,4.75,6,7.466666667,5.03,5.23,4.85,5.59,5.96,5.33,4.92,4.255555556,6.346666667,4.13,6.33,4,7.35,6.35,4.63,5.13,7.4,4.28,4.233333333,4.3125,6.18,4.3,4.47,4.88,4.5,2.96,2.1,3.7,3.62,5.42,3.8,5.5,3.27,3.36,3.266666667,2.265,3.1,2.51,2.51,4.4,2.64,4.38,4.53,2.29,2.87,3.395,3.26,2.77,3.22,4.31,4.73,4.05,3.48,4.8,4.7,3.05,4.21,5.95,4.39,4.55,4.27,4.955,4.65,3.32,3.48,3.828571429,4.69,4.68,3.76,3.91,4,4.41,4.19,4.733333333,4.32,2.83,3.41,4.42,3.47,3.84,4.39)
x.number <- c(69,62,8,80,13,12,2,22,19,49,840,44,31,56,33,58,91,8,15,86,11,69,12,24,32,27,1,4,26,4,28,33,1516,41,20,58,44,29,58,14,3,3,6,3,26,52,26,29,92,30,18,11,27,19,38,78,57,52,17,45,56,7,37,7,14,13,164,76,82,14,273,122,662,434,126,374,1017,522,374,602,164,5,191,243,134,70,23,130,306,516,414,236,172,164,92,53,50,17,22,27,92,48,30,55,28,296,35,12,350,17,22,53,97,62,92,272,242,170,37,220,452,270,392,314,150,232)
df <- df[df$totalinf < 750,]
a <- 9
b <- 0.07
c <- 3
ggplot(data=df,aes(x=x.number,y=y.size))+ geom_point()+ stat_function(fun=function(x)a*exp(-x*b) + c, color = "blue")
I use a ML estimator to initialize the function using the estimates
a = 9; b = 0.07; c = 3; sigma = 1
expreg <- function(a,b,c, sigma){
y.pred <- a * exp(-x.number*b) + c
ll <- -sum(dnorm(y.size, mean = y.pred, sd = sigma, log=TRUE ))
ll
}
mle2.expreg.model <- mle(expreg, start = list(a = 9, b = 0.07, c = 3 , sigma = 1))
summary(mle2.expreg.model)
Coefficients:
Estimate Std. Error
a 8.667305 974.16243176
b 12.671940 NaN
c 4.488451 0.12466034
sigma 1.382550 0.08814796
The b estimates are nearly 10x difference in order of magnitude. Needless to say, the curve looks quite flat with the new estimates