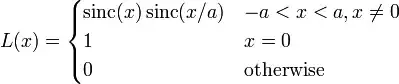0

My question

I have a question. I tried many time with different codes but i did not find answer. I am not sure in every time about my answer. I wonder how to find answer using with matlab. I tried codes:

A=[14 12 10 12 11 10 13 7 9 16; 
16 14 13 13 12 6 9 10 13 11; 
16 14 12 13 11 8 9 11 11 3; 
13 13 12 12 15 11 12 12 4 3, 
16 9 4 12 14 8 9 21 11 5; 
16 15 15 12 8 8 5 5 6 12; 
12 11 13 11 13 4 4 3 2 5; 
7 7 13 13 14 4 4 3 4 5; 
8 11 5 12 12 4 5 4 4 5; 
14 14 12 6 12 5 2 3 5 3]
%my first try
kernel = -1 * ones(3);
kernel(2,2) = 8;  % Now kernel = [-1,-1,-1; -1,8,-1; -1,-1,-1]
output = conv2(A,kernel,'same');
%my second try
b=[0 1 0; 1 -4 1; 0 1 0]
 c=conv2(A,b,'valid')
%my third try
b=[-1,-1,-1; -1,8,-1; -1,-1,-1]
c=conv2(A,b,'valid')
%my 4th try
A=uint8(A);
H = fspecial('laplacian',0,2)
T=imfilter(A,H);

I would be glad if you help.

Wolfie
  • 27,562
  • 7
  • 28
  • 55
Deeper Blue
  • 7
  • 6
  • 1
    Please type out your question, don’t post a screen shot of your teacher’s question. – Cris Luengo Nov 15 '20 at 14:59
  • 1
    There are many ways to discretize the Laplace operator, which one your teacher is thinking of would be known by looking at your text book and/or lecture notes. – Cris Luengo Nov 15 '20 at 15:00
  • @CrisLuengo I tried all of them but i don't find answer to this question. – Deeper Blue Nov 15 '20 at 15:11
  • Why do you think your answers were incorrect? – beaker Nov 15 '20 at 16:09
  • 1
    Also “the pixel at (4,4)” could be 1-based indexing as in MATLAB, or 0-based indexing as in most other languages. – Cris Luengo Nov 15 '20 at 16:23
  • @CrisLuengo That is not wrong sign. I tried different laplacian mask to find answer but it didn't work. – Deeper Blue Nov 15 '20 at 16:32
  • @beaker because my answers are not in options. – Deeper Blue Nov 15 '20 at 16:34
  • I do not know much about image processing in matlab. I would be glad if you could help. – Deeper Blue Nov 15 '20 at 16:53
  • You’re right, the 1st and 3rd attempts have wrong sign. The value in the middle must be negative. – Cris Luengo Nov 15 '20 at 17:01
  • @CrisLuengo I agree with you absolutely but i still don't understand how to find true answer. The question seems easy but I couldn't. – Deeper Blue Nov 15 '20 at 17:26
  • The aim is finding the matlab code that gives the correct answer to this question. For example, i gave you a 50x50 matrix. Will you calculate manually one by one? – Deeper Blue Nov 15 '20 at 17:39
  • 1
    Regardless of the size of the matrix, you're still only calculating over the size of the kernel for each pixel. – beaker Nov 15 '20 at 18:01
  • I think, you have to move the Laplacian filter through the matrix to solving. If you can solve it, I will be glad if you help. I do not know much about the subject. – Deeper Blue Nov 15 '20 at 18:11
  • This question is unfortunately going to be dependent on the derived Laplacian filter kernel used as the others have suggested. – MichaelTr7 Nov 15 '20 at 23:04
  • Also maybe edit your question to state that you need to prove this using MATLAB as you have told me on your other questions. – MichaelTr7 Nov 15 '20 at 23:06
  • I have a no idea about how to find answer of this question. I've tried all the laplace codes. – Deeper Blue Nov 15 '20 at 23:19
  • The typical convolution/filtering for images will use the `same` property this uses the padding usually considered. – MichaelTr7 Nov 16 '20 at 00:09

1 Answers1

1

By Only Taking Pixels of Interest:

Pixel (4,4) → Pixel (5,5) in MATLAB

Image Array

To expand on @beaker's point you only need the neighbourhood that surrounds the pixel. This neighbourhood will be dependent on the filter kernel size. The size of the neighbourhood including the pixel of interest should be the same size as the filter kernel. For this question, it would proceed as follows. You can simply multiply the corresponding/overlapping components take the sum of all the products to get the resultant pixel value. This is essentially taking a snippet of the filter/convolution process.

Neighbourhood = [12 15 11; 12 14 8; 12 8 8];
Laplacian_Kernel = [0 -1 0; -1 4 -1; 0 -1 0];
Result = sum(Neighbourhood.*Laplacian_Kernel,'all');
Result

Common Laplacian Filter Kernels:

Here are some of my attempts at trying various common Laplacian filter kernels, but without more specifics about your question, you should consult this answer just as a means for practicing or using this as a playground script. Discrete derivatives can be calculated in several ways which are visually shown by the positive (red) and negative (blue) complementary components in the Laplacian kernels. One thing to take into account is the start/base indexing. In MATLAB the start/base indexing is 1. Therefore, the top-left pixel is (1,1) opposed to (0,0). Knowing this fact we can infer that pixel (4,4) in the question refers to pixel (5,5) in terms of MATLAB arrays. For more details on convolution and filtering see this question: Moving Filter/Mask Across Given Image (No Function)

Common Laplacian Filter Kernels

A = [14 12 10 12 11 10 13 7 9 16; 
16 14 13 13 12 6 9 10 13 11; 
16 14 12 13 11 8 9 11 11 3; 
13 13 12 12 15 11 12 12 4 3; 
16 9 4 12 14 8 9 21 11 5; 
16 15 15 12 8 8 5 5 6 12; 
12 11 13 11 13 4 4 3 2 5; 
7 7 13 13 14 4 4 3 4 5; 
8 11 5 12 12 4 5 4 4 5; 
14 14 12 6 12 5 2 3 5 3];

%Common Laplacian filter kernels%
%Kernel 1%
Laplacian_Kernel_1 = [0 -1 0; -1 4 -1; 0 -1 0];
Filtered_Image_1 = conv2(A,Laplacian_Kernel_1,'same');
Result_1 = Filtered_Image_1(5,5);
fprintf("Filter 1: %d\n",Result_1);

%Kernel 2%
Laplacian_Kernel_2 = [-1 -1 -1; -1 8 -1; -1 -1 -1];
Filtered_Image_2 = conv2(A,Laplacian_Kernel_2,'same');
Result_2 = Filtered_Image_2(5,5);
fprintf("Filter 2: %d\n",Result_2);

%Kernel 3%
Laplacian_Kernel_3 = [1 -2 1; -2 4 -2; 1 -2 1];
Filtered_Image_3 = conv2(A,Laplacian_Kernel_3,'same');
Result_3 = Filtered_Image_3(5,5);
fprintf("Filter 3: %d\n",Result_3);

%Kernel 4%
Laplacian_Kernel_4 = [1 2 1; 2 -12 2; 1 2 1];
Filtered_Image_4 = conv2(A,Laplacian_Kernel_4,'same');
Result_4 = Filtered_Image_4(5,5);
fprintf("Filter 4: %d\n",Result_4);

Output Results 1

Negatives of the Laplacian filter kernels are also valid:

Negative Laplacian Filter Kernels

%Negative Laplacian filter kernels%
%Kernel 1%
Laplacian_Kernel_1 = -[0 -1 0; -1 4 -1; 0 -1 0];
Filtered_Image_1 = conv2(A,Laplacian_Kernel_1,'same');
Result_1 = Filtered_Image_1(5,5);
fprintf("Filter 1: %d\n",Result_1);

%Kernel 2%
Laplacian_Kernel_2 = -[-1 -1 -1; -1 8 -1; -1 -1 -1];
Filtered_Image_2 = conv2(A,Laplacian_Kernel_2,'same');
Result_2 = Filtered_Image_2(5,5);
fprintf("Filter 2: %d\n",Result_2);

%Kernel 3%
Laplacian_Kernel_3 = -[1 -2 1; -2 4 -2; 1 -2 1];
Filtered_Image_3 = conv2(A,Laplacian_Kernel_3,'same');
Result_3 = Filtered_Image_3(5,5);
fprintf("Filter 3: %d\n",Result_3);

%Kernel 4%
Laplacian_Kernel_4 = -[1 2 1; 2 -12 2; 1 2 1];
Filtered_Image_4 = conv2(A,Laplacian_Kernel_4,'same');
Result_4 = Filtered_Image_4(5,5);
fprintf("Filter 4: %d\n",Result_4);

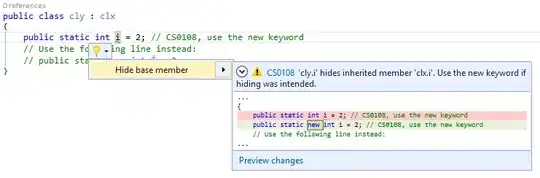
Output Results 2

Extension: Results of Laplacian Filters and Their Corresponding Negatives

Laplacian Filtered Test Image

Laplacian Filtering Playground Script:

Image = rgb2gray(imread("peppers.png"));

subplot(1,3,1); imshow(Image);
title("Original Image");

Laplacian_Kernel = [0 -1 0; -1 4 -1; 0 -1 0];
Filtered_Image_1 = conv2(Image,Laplacian_Kernel_1,'same');
subplot(1,3,2); imshow(Filtered_Image_1);
title("Laplacian Filtered Image");

Negative_Laplacian_Kernel = -[0 -1 0; -1 4 -1; 0 -1 0];
Filtered_Image_2 = conv2(Image,Negative_Laplacian_Kernel,'same');
subplot(1,3,3); imshow(Filtered_Image_2);
title("Negative Laplacian Filtered Image");

Ran using MATLAB R2019b

MichaelTr7
  • 4,737
  • 2
  • 6
  • 21