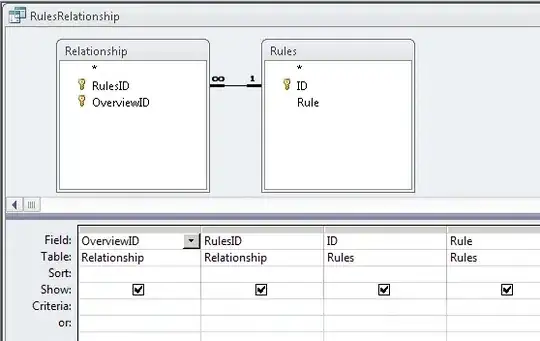
This is just a plotting issue. The plt.plot function draws by default a line plot without markers. Since your data is not sorted by x variable, the line jumps back and forth making the result look messy. I generated sample data and plotted with plt.plot defaults and then by hiding the line, and adding markers. The results are
With default plt.plot arguments
Rest of the code below (not repeated for convenience)
spline_basis = patsy.cr(x, df=3)
model = LinearRegression().fit(spline_basis, y)
y_spline = model.predict(spline_basis)
plt.scatter(x, y)
plt.plot(x, y_spline, color="red")
plt.show()
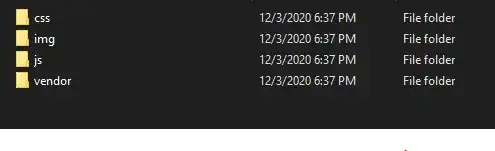
With plt.plot when marker='.' and ls=''
Rest of the code below (not repeated for convenience)
spline_basis = patsy.cr(x, df=3)
model = LinearRegression().fit(spline_basis, y)
y_spline = model.predict(spline_basis)
plt.scatter(x, y)
plt.plot(x, y_spline, ls="", marker=".", color="red") # Only this changed
plt.show()
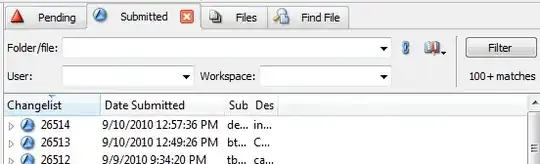
By reordering data
Rest of the code below (not repeated for convenience)
If you want to draw a line plot, you could just reorder the data for fitting, like this:
spline_basis = patsy.cr(x, df=3)
model = LinearRegression().fit(spline_basis, y)
y_spline = model.predict(spline_basis)
plt.scatter(x, y)
xsorted, ysorted = zip(*[(X, Y) for (X, Y) in sorted(zip(x, y_spline))]) # simple reordering
plt.plot(xsorted, ysorted, color="red")
plt.show()

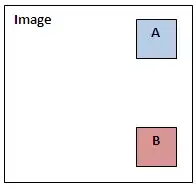
By using new data for prediction
Usually, models are created for prediction. The idea is to create model with training data and then use the model with some new data. This new data can be anything. If it is sorted, it can be plotted as lineplot. In this case, you can create new x-values, for example
new_x = np.linspace(10, 100, 100)
and calculate the predicted y-values for them. For this, you need to know (and save) only few values. Actually, just df, lower_bound, upper_bound and the 4 floats from model._coef.
# Fit model
spline_basis = patsy.cr(x, df=3, lower_bound=x.min(), upper_bound=x.max())
model = LinearRegression().fit(spline_basis, y)
y_train = model.predict(spline_basis)
# Use model
new_x = np.linspace(10, 100, 100) # 100 points
spline_basis_new = patsy.cr(new_x, df=3, lower_bound=x.min(), upper_bound=x.max())
new_y = model.predict(spline_basis_new)
plt.scatter(x, y)
plt.plot(x, y_train, color="red", ls="", marker=".")
plt.plot(new_x, new_y, color="green")
plt.show()
Rest of the code
from matplotlib import pyplot as plt
import numpy as np
import patsy
from sklearn.linear_model import LinearRegression
def dummy_data():
np.random.seed(1)
x = np.random.choice(np.arange(18, 81), size=4000)
def model(x):
a = 83 / 107520
b = -895 / 5376
c = 17747 / 1680
d = -622 / 7
return a * x ** 3 + b * x ** 2 + c * x + d
def noisemodel(x):
an = -0.0591836734693878
bn = 5.25510204081633
cn = -31.6326530612245
return an * x ** 2 + bn * x + cn
y = model(x)
ynoise = np.array([np.random.randn() * noisemodel(_) for _ in x])
return x, y + ynoise
x, y = dummy_data()