Shifting angles while using Atan2

Question

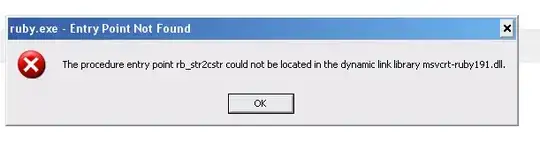
I am currently using Atan2 to calculate the player heading angle.

however after some trial and error I discovered that the in-game angle's are rather different to that of a "normal" lay out :

        ReturnedAngle = Math.Atan2(Y2 - Y1, X2 - X1);  /// ArcTan2 the difference in our Y axis is always passed first followed by X

        ReturnedAngle = (180 / Math.PI) * ReturnedAngle; /// Converting our radians to Degrees the convervion ends at 358 not the full 360 degrees.

        ReturnedAngle = Math.Round(ReturnedAngle + 360, MidpointRounding.AwayFromZero) % 360; /// MOD and round our angle.

Above is the C# code I am using to calc the heading angle. My questions is how would I go about converting this angle from the "normal" angle system to the in-game one.

Could you show Y and X axes direction on the left picture? Where are points (100,100) and (100, -100)? — MBo, Nov 11 '20 at 09:53

John Alexiou · Accepted Answer · 2020-11-11T16:38:11.613

1

I think this is your situation. You have a right-hand coordinate system, but you are measuring a clock-wise angle, which is inconsistent.

In any case, draw a small positive angle from 360 (red below) to form a right triangle (purple below) with positive sides.

To measure the angle θ of the triangle, measure the short side Δx and the long side Δy and compute.

var θ = Math.Atan2(Δx, Δy);

This would work for any positive or negative values for the two sides. For example, if the angle goes above 90° then Δy would flip signs, as your target point is going to be below the origin. But the beauty of Atan2() is that you don't need to worry about these cases as it works on all four quadrants if you make it work for a small positive angle.

In reverse you have

var Δx = R*Math.Sin(Θ);
var Δy = R*Math.Cos(Θ);

where R is the distance between the target and the reference point.

edited Nov 11 '20 at 16:38

answered Nov 11 '20 at 08:45

John Alexiou

28,472
11
77
133

Thanks for the answer but I can't say I following understand. I have both the players current location and the location of the Way-point the players is heading. Could you possibly explain in a mathematical formula ? – MrClear Nov 11 '20 at 09:32
You need to add the direction of x and y axis on the diagram to be able to derive a formula. Does y go up or down? – John Alexiou Nov 11 '20 at 15:51
Ah yes, It's as normal such that if you were facing 360 degrees (in-game) and moved forward you would increase your Y axis. And if you were facing 90 degrees (in-game) and moved forward you would increase your X axis. – MrClear Nov 11 '20 at 16:23

score 1 · Answer 2 · answered Nov 11 '20 at 11:38

Math.Atan2(Y2 - Y1, X2 - X1) computes the angle anticlockwise from the x axis. Math.Atan2(X2 - X1, Y2 - Y1) computes the angle clockwise from the y axis, which is what you want.

The 'clockwise from north' convention is used in navigation and mapping. Over the years I've found that it easiest to think in terms of vectors having components north, east. This means that atan2 is called the same way, that is, to get the direction of q from p:

dirn = atan2( q[1]-p[1], q[0]-p[0]);

If you are thinking of p and q as x,y vectors this gives you the angle anti-clockwise from the x axis. If you are thinking of p and q as n,e vectors it gives you the angle clockwise from north.

It also means that the formulae for a rotation matrix is the same. To rotate through an angle a, you use the matrix

R = ( cos(a)  -sin(a) )
    ( sin(a)   cos(a) )

Again, if you are thinking of the vectors as being x,y then applying R rotates through and angle a, anti-clockwise from the axis, while if you think of vectors as being n,e applying R rotates through an angle a, clockwise from north.

Hey mate, thanks for the response after implementing your method it seems to path in the opposite direction. I am calling it as follows : ReturnedAngle = Math.Atan2(X2 - X1, Y2 - Y1); I then simply convert the returned value to degrees (from radians) Then I add 360 degree to that angle and mob it by 360. I then take that returned angle and set it in-game... Apologies I know my maths isn't the sharpest the shift in angles / direction is throwing me off. Any further suggestions? — MrClear, Nov 11 '20 at 14:42

Shifting angles while using Atan2

2 Answers2