Plot DelaunayTriangulation in Mathematica

Question

Considering the following example (from Sjoerd Solution on plotting a ConvexHull)

Needs["ComputationalGeometry`"]
pts = RandomReal[{0, 10}, {60, 2}];
dtpts=DelaunayTriangulation[pts]

I would now like to plot the DelaunayTriangulation for a set of point but can`t figure out the Plot syntax using Graphics.

Thoughts ?

score 4 · Answer 1 · answered Jun 24 '11 at 15:39

Method one, using polygons like Sjoerd, but without the problem caused by points on the convex hull:

Graphics[{FaceForm[], EdgeForm[Black], 
  Polygon[pts[[#]] & /@ 
    DeleteCases[dtpts, {i_, _} /; MemberQ[ConvexHull[pts], i]][[All, 
      2]]], Red, Point[pts]}]

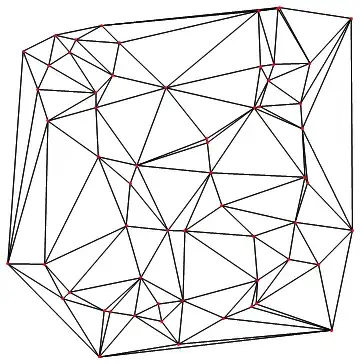
Method two, using lines connecting the adjacent points:

edges[pts_, {a_, l_List}] := {pts[[a]], #} & /@ pts[[l]]
Graphics[{Line[edges[pts, #]] & /@ dtpts, Red, Point[pts]}]

Both of these methods result in duplicated primitives (three polygons or two lines, from using each point as a starting point.)

We can modify the data slightly and use built in visualization functions:

Graphics[{FaceForm[], EdgeForm[Black], 
  Cases[Normal[
    ListDensityPlot[{##, 0.} & @@@ pts, Mesh -> All]], _Polygon, 
   Infinity], Red, Point[pts]}, ImageSize -> 175]

enter image description here

I already changed my solution 15 minutes ago. I have a polygon solution ready for an update too... — Sjoerd C. de Vries, Jun 24 '11 at 15:53

Sjoerd C. de Vries · Accepted Answer · 2011-06-24T15:57:56.437

3

Graphics[
  GraphicsComplex[
    pts, 
    {
      Function[{startPt, finishPts},Line[{startPt, #}] & /@ finishPts] @@@ dtpts, 
      Red, Point@Range[Length@pts]
    }
   ]
  ]

enter image description here

And if you need real polygons:

Graphics[
 GraphicsComplex[
  pts, 
  {EdgeForm[Black], 
   Function[{startPt, finishPts}, 
      {FaceForm[RGBColor[RandomReal[], RandomReal[], RandomReal[]]], 
        Polygon[{startPt, ##}]} & @@@ 
          Transpose[{Drop[finishPts, 1], 
                     Drop[RotateRight@finishPts, 1]
                    }
          ]
         ] @@@ dtpts, 
   Red, Point@Range[Length@pts]
  }
 ]
]

enter image description here

edited Jun 24 '11 at 15:57

answered Jun 24 '11 at 14:53

Sjoerd C. de Vries

16,122
3
42
94

@Sjoerd, thank you again ! I edited my question to describe dtpts. – 500 Jun 24 '11 at 14:58
New interpretation of the output. This is better – Sjoerd C. de Vries Jun 24 '11 at 15:22
Well, it still isn't perfect. The way they are generated, all polygons appear multiple times in the triangulation results. But that's a question of sorting and using Union. – Sjoerd C. de Vries Jun 24 '11 at 16:23
@Sjoerd, would you know how to count the number of edges ? – 500 Jun 24 '11 at 16:43
@500 brett has defined an edges function. You could use that, sort the edge points, delete duplicates, count. Easy. – Sjoerd C. de Vries Jun 24 '11 at 17:30
I think the number of edges should be `Total[Length/@ dtpts[[All,2]]]/2`. – Brett Champion Jun 24 '11 at 18:42

score 1 · Answer 3 · answered Aug 24 '11 at 09:32

I like Sjoerd's use of GraphicsComplex, but I don't see the need for the baroque code in the middle.

This appears to work just fine:

Needs["ComputationalGeometry`"]
pts = RandomReal[{0, 10}, {60, 2}];
dtpts = DelaunayTriangulation[pts];

Lines

Graphics[GraphicsComplex[
  pts,
  {Line /@ Thread /@ dtpts, Red, Point@Range@Length@pts}
]]

enter image description here

Polygons

Graphics[GraphicsComplex[
  pts,
  {
    EdgeForm[Black],
    ( {FaceForm[RGBColor @@ RandomReal[1, 3]], Polygon@#} & /@ 
      Append @@@ Thread@{Partition[#2, 2, 1], #} & ) @@@ dtpts,
    Red,
    Point@Range[Length@pts]
  }
]]

enter image description here

Plot DelaunayTriangulation in Mathematica

3 Answers3

Lines

Polygons

Linked